题目内容
如图, 与
与 都是等边三角形,在这个图形中,有两个三角形一定是全等的,利用符号“
都是等边三角形,在这个图形中,有两个三角形一定是全等的,利用符号“ ”可以表示为( )
”可以表示为( )

A. B.
B.
C. D.
D.
【答案】
D
【解析】
试题分析:根据 与
与 都是等边三角形可得AC=AE,AB=AD,∠EAC=∠BAD=60°,
都是等边三角形可得AC=AE,AB=AD,∠EAC=∠BAD=60°,
则可得∠DAC=∠BAE=120°,即可根据“SAS”证得 。
。
∵ 与
与 都是等边三角形
都是等边三角形
∴AC=AE,AB=AD,∠EAC=∠BAD=60°,
∴∠BAC=60°,
∴∠DAC=∠BAE=120°,
∴ ,
,
故选D.
考点:本题考查了等边三角形的性质,全等三角形的判定
点评:判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 ,
, 都是等边三角形,求证
都是等边三角形,求证 .
.
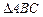 与
与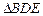 都是等边三角形,点
都是等边三角形,点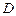 在边
在边 上(不与
上(不与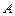 、
、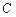 重合),
重合),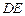 与
与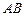 相交于点
相交于点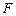 .
.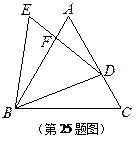

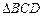 ∽
∽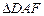 ;
;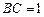 ,设
,设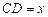 ,
,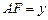 ;
;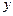 关于
关于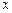
 的函数解析式及定义域;
的函数解析式及定义域;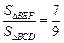 ?
? 与
与 均是等边三角形,连接BE、CD.请在图中找出一条与
均是等边三角形,连接BE、CD.请在图中找出一条与 长度相等的线段,并证明你的结论.
长度相等的线段,并证明你的结论.
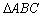 与
与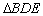 都是等边三角形,点
都是等边三角形,点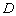 在边
在边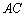 上(不与
上(不与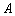 、
、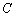 重合),
重合),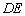 与
与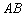 相交于点
相交于点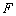 .
.
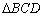 ∽
∽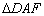 ;
;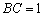 ,设
,设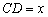 ,
,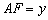 ;
;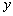 关于
关于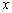 的函数解析式及定义域;
的函数解析式及定义域;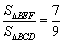 ?
?