题目内容
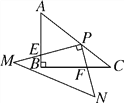
【题目】如图，△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，且A、C、B在同一直线上，有如下结论：①△ACE≌△DCB；②CM＝CN；③AC＝DN；④PC平分∠APB；⑤∠APD＝60°，其中正确结论有（ ）
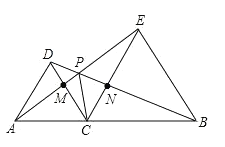
A.①②③④⑤B.①②④⑤C.①②③⑤D.①②⑤
【答案】B
【解析】
①利用等边三角形的性质根据SAS证
；②利用ASA证
可得结论；③在
，可得
，易知
；④过点C作
于点Q，
于点H ，由及三角形面积公式可得
，可得
平分
；⑤根据三角形的外角的性质可得结论.
解：①
△DAC和△EBC均是等边三角形，
，
在
和
中
可得①正确；
②由①知，
，
在和
中
可得②正确；
③由②得
，在，，
，可得③错误；
④过点C作于点Q，于点H，
由②得，
，
，
，
平分，可得④正确；
⑤ 
可得⑤正确.
故选：B
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
