题目内容
 如图,在某圆锥形灯罩的轴截面中,OA=OB,∠AOB=60°,已知一平顶房间高度为3米,若此灯罩的光源O发出的光线到达该房间水平地面的最大圆面面积为2.25π平方米(假设该水平地面足够大),则点O到此房间顶端的距离约为
如图,在某圆锥形灯罩的轴截面中,OA=OB,∠AOB=60°,已知一平顶房间高度为3米,若此灯罩的光源O发出的光线到达该房间水平地面的最大圆面面积为2.25π平方米(假设该水平地面足够大),则点O到此房间顶端的距离约为
- A.0.3米
- B.0.35米
- C.0.4米
- D.0.45米
C
分析:首先判定△OAB是等边三角形,然后延长OA交地面于点A′,延长OB交地面于点B′,从而得到△OA′B′和△OAB相似,根据光线到达地面圆的面积求出半径从而得到A′B′的长度,再根据等边三角形的性质求出点O到A′B′的距离,即可得解.
解答: 解:如图,∵OA=OB,∠AOB=60°,
解:如图,∵OA=OB,∠AOB=60°,
∴△OAB是等边三角形,
延长OA交地面于点A′,延长OB交地面于点B′,可得△OA′B′∽△OAB,
设光线到达该房间水平地面的最大圆的半径为r米,
则πr2=2.25π,
解得r=1.5,
∴A′B′=2r=2×1.5=3米,
根据等边三角形的性质,点O到A′B′的距离为3× =2.598米,
=2.598米,
∴点O到此房间顶端的距离约为3-2.598=0.402≈0.4米.
故选C.
点评:本题考查了相似三角形的应用,等边三角形的判定与性质,以及圆的面积公式,难度不大,判定出等边三角形是解题的关键.
分析:首先判定△OAB是等边三角形,然后延长OA交地面于点A′,延长OB交地面于点B′,从而得到△OA′B′和△OAB相似,根据光线到达地面圆的面积求出半径从而得到A′B′的长度,再根据等边三角形的性质求出点O到A′B′的距离,即可得解.
解答:
 解:如图,∵OA=OB,∠AOB=60°,
解:如图,∵OA=OB,∠AOB=60°,∴△OAB是等边三角形,
延长OA交地面于点A′,延长OB交地面于点B′,可得△OA′B′∽△OAB,
设光线到达该房间水平地面的最大圆的半径为r米,
则πr2=2.25π,
解得r=1.5,
∴A′B′=2r=2×1.5=3米,
根据等边三角形的性质,点O到A′B′的距离为3×
 =2.598米,
=2.598米,∴点O到此房间顶端的距离约为3-2.598=0.402≈0.4米.
故选C.
点评:本题考查了相似三角形的应用,等边三角形的判定与性质,以及圆的面积公式,难度不大,判定出等边三角形是解题的关键.

练习册系列答案
相关题目
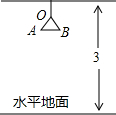 (2012•龙湾区二模)如图,在某圆锥形灯罩的轴截面中,OA=OB,∠AOB=60°,已知一平顶房间高度为3米,若此灯罩的光源O发出的光线到达该房间水平地面的最大圆面面积为2.25π平方米(假设该水平地面足够大),则点O到此房间顶端的距离约为( )
(2012•龙湾区二模)如图,在某圆锥形灯罩的轴截面中,OA=OB,∠AOB=60°,已知一平顶房间高度为3米,若此灯罩的光源O发出的光线到达该房间水平地面的最大圆面面积为2.25π平方米(假设该水平地面足够大),则点O到此房间顶端的距离约为( )