题目内容
(1)如图(1),BD、CD是∠ABC和∠ACB的角平分线且相交于点D,请猜想∠A与∠BDC之间的数量关系,并说明理由.
(2)如图(2),BD、CD是∠ABC和∠ACB外角的平分线且相交于点D.请猜想∠A与∠BDC之间的数量关系,并说明理由.
(3)如图(3),BD、CD是∠ABC和∠ACB外角的平分线且相交于点D,请猜想∠A与∠BDC之间的数量关系,并说明理由.
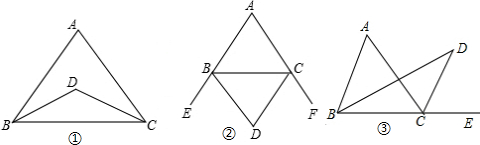
解:(1)∠BDC=90°+ ∠A.理由如下:
∠A.理由如下:
∵BD、CD是∠ABC和∠ACB的角平分线,
∴∠DBC= ∠ABC,∠DCB=
∠ABC,∠DCB=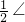 ACB,
ACB,
∵∠D=180°-(∠DBC+∠DCB),即∠D=180°- (∠ABC+∠ACB),
(∠ABC+∠ACB),
而∠ABC+∠ACB=180°-∠A,
∴∠D=180°- (180°-∠A),
(180°-∠A),
即∠BDC=90°+ ∠A;
∠A;
(2))∠BDC=90°- ∠A.理由如下:
∠A.理由如下:
∵BD、CD是∠ABC和∠ACB外角的平分线,
∴∠DBC= ∠EBC,∠DCB=
∠EBC,∠DCB=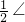 FCB,
FCB,
∴∠DBC= (180°-∠ABC),∠DCB=
(180°-∠ABC),∠DCB= (180°-∠ACB),
(180°-∠ACB),
∴∠D=180°-(∠DBC+∠DCB),即∠D=180°- (360°-∠ABC-∠ACB),
(360°-∠ABC-∠ACB),
而∠ABC+∠ACB=180°-∠A,
∴∠D=180°- (360°-180°+∠A),
(360°-180°+∠A),
即∠BDC=90°- ∠A;
∠A;
(3)∠BDC= ∠A.理由如下:
∠A.理由如下:
∵BD、CD是∠ABC和∠ACB外角的平分线,
∴∠DBC= ∠ABC,∠DCE=
∠ABC,∠DCE= ACE,
ACE,
∵∠DCE=∠DBC+∠D,
∴∠D= ∠ACE-
∠ACE- ∠ABC=
∠ABC= (∠ACE-∠ABC)=
(∠ACE-∠ABC)= ∠A.
∠A.
分析:(1)根据角平分线的定义得到∠DBC= ∠ABC,∠DCB=
∠ABC,∠DCB=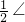 ACB,再根据三角形内角和定理得∠D=180°-
ACB,再根据三角形内角和定理得∠D=180°- (∠ABC+∠ACB),然后把∠ABC+∠ACB=180°-∠A代入即可得到∠BDC=90°+
(∠ABC+∠ACB),然后把∠ABC+∠ACB=180°-∠A代入即可得到∠BDC=90°+ ∠A;
∠A;
(2)根据角平分线的定义得到∠DBC= ∠EBC,∠DCB=
∠EBC,∠DCB=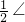 FCB,利用邻补角的定义有∠DBC=
FCB,利用邻补角的定义有∠DBC= (180°-∠ABC),∠DCB=
(180°-∠ABC),∠DCB= (180°-∠ACB),则∠D=180°-(∠DBC+∠DCB),即∠D=180°-
(180°-∠ACB),则∠D=180°-(∠DBC+∠DCB),即∠D=180°- (360°-∠ABC-∠ACB),然后把∠ABC+∠ACB=180°-∠A代入整理得到∠BDC=90°-
(360°-∠ABC-∠ACB),然后把∠ABC+∠ACB=180°-∠A代入整理得到∠BDC=90°- ∠A;
∠A;
(3)根据角平分线的定义得到∠DBC= ∠ABC,∠DCE=
∠ABC,∠DCE=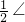 ACE,根据三角形外角性质得∠DCE=∠DBC+∠D,所以∠D=
ACE,根据三角形外角性质得∠DCE=∠DBC+∠D,所以∠D= ∠ACE-
∠ACE- ∠ABC=
∠ABC= (∠ACE-∠ABC)=
(∠ACE-∠ABC)= ∠A.
∠A.
点评:本题考查了三角形内角和定理:三角形内角和为180°.也考查了三角形外角性质以及角平分线的定义.
 ∠A.理由如下:
∠A.理由如下:∵BD、CD是∠ABC和∠ACB的角平分线,
∴∠DBC=
 ∠ABC,∠DCB=
∠ABC,∠DCB=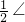 ACB,
ACB,∵∠D=180°-(∠DBC+∠DCB),即∠D=180°-
 (∠ABC+∠ACB),
(∠ABC+∠ACB),而∠ABC+∠ACB=180°-∠A,
∴∠D=180°-
 (180°-∠A),
(180°-∠A),即∠BDC=90°+
 ∠A;
∠A;(2))∠BDC=90°-
 ∠A.理由如下:
∠A.理由如下:∵BD、CD是∠ABC和∠ACB外角的平分线,
∴∠DBC=
 ∠EBC,∠DCB=
∠EBC,∠DCB=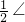 FCB,
FCB,∴∠DBC=
 (180°-∠ABC),∠DCB=
(180°-∠ABC),∠DCB= (180°-∠ACB),
(180°-∠ACB),∴∠D=180°-(∠DBC+∠DCB),即∠D=180°-
 (360°-∠ABC-∠ACB),
(360°-∠ABC-∠ACB),而∠ABC+∠ACB=180°-∠A,
∴∠D=180°-
 (360°-180°+∠A),
(360°-180°+∠A),即∠BDC=90°-
 ∠A;
∠A;(3)∠BDC=
 ∠A.理由如下:
∠A.理由如下:∵BD、CD是∠ABC和∠ACB外角的平分线,
∴∠DBC=
 ∠ABC,∠DCE=
∠ABC,∠DCE=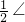 ACE,
ACE,∵∠DCE=∠DBC+∠D,
∴∠D=
 ∠ACE-
∠ACE- ∠ABC=
∠ABC= (∠ACE-∠ABC)=
(∠ACE-∠ABC)= ∠A.
∠A.分析:(1)根据角平分线的定义得到∠DBC=
 ∠ABC,∠DCB=
∠ABC,∠DCB=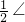 ACB,再根据三角形内角和定理得∠D=180°-
ACB,再根据三角形内角和定理得∠D=180°- (∠ABC+∠ACB),然后把∠ABC+∠ACB=180°-∠A代入即可得到∠BDC=90°+
(∠ABC+∠ACB),然后把∠ABC+∠ACB=180°-∠A代入即可得到∠BDC=90°+ ∠A;
∠A;(2)根据角平分线的定义得到∠DBC=
 ∠EBC,∠DCB=
∠EBC,∠DCB=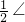 FCB,利用邻补角的定义有∠DBC=
FCB,利用邻补角的定义有∠DBC= (180°-∠ABC),∠DCB=
(180°-∠ABC),∠DCB= (180°-∠ACB),则∠D=180°-(∠DBC+∠DCB),即∠D=180°-
(180°-∠ACB),则∠D=180°-(∠DBC+∠DCB),即∠D=180°- (360°-∠ABC-∠ACB),然后把∠ABC+∠ACB=180°-∠A代入整理得到∠BDC=90°-
(360°-∠ABC-∠ACB),然后把∠ABC+∠ACB=180°-∠A代入整理得到∠BDC=90°- ∠A;
∠A;(3)根据角平分线的定义得到∠DBC=
 ∠ABC,∠DCE=
∠ABC,∠DCE=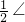 ACE,根据三角形外角性质得∠DCE=∠DBC+∠D,所以∠D=
ACE,根据三角形外角性质得∠DCE=∠DBC+∠D,所以∠D= ∠ACE-
∠ACE- ∠ABC=
∠ABC= (∠ACE-∠ABC)=
(∠ACE-∠ABC)= ∠A.
∠A.点评:本题考查了三角形内角和定理:三角形内角和为180°.也考查了三角形外角性质以及角平分线的定义.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.