题目内容
 (2006•厦门模拟)如图,在平面直角坐标系中,已知点A(1,2),B(3,2),C(4,3),D(2,6),E(3,5)且以点D、E、F为顶点的三角形与△ABC全等,那么点F的坐标为
(2006•厦门模拟)如图,在平面直角坐标系中,已知点A(1,2),B(3,2),C(4,3),D(2,6),E(3,5)且以点D、E、F为顶点的三角形与△ABC全等,那么点F的坐标为F1(2,8),F2(0,6),F3(5,5),F4(3,3)
F1(2,8),F2(0,6),F3(5,5),F4(3,3)
.分析:设点F的坐标是(x,y).
分类讨论:①△FDE≌△ABC,利用两点间的距离公式列出关于x、y的二元一次方程组,通过解方程组即可求得点F的坐标;
②当△FED≌△ABC时,利用两点间的距离公式列出关于x、y的二元一次方程组,通过解方程组即可求得点F的坐标.
分类讨论:①△FDE≌△ABC,利用两点间的距离公式列出关于x、y的二元一次方程组,通过解方程组即可求得点F的坐标;
②当△FED≌△ABC时,利用两点间的距离公式列出关于x、y的二元一次方程组,通过解方程组即可求得点F的坐标.
解答: 解:设点F的坐标是(x,y).
解:设点F的坐标是(x,y).
∵A(1,2),B(3,2),C(4,3),D(2,6),E(3,5),
∴AB=2,BC=
,AC=
,DE=
;
①当△FDE≌△ABC时,FE=AC=
,DF=BA=2,则
,
解得,
或
;
∴F1(2,8),F2(0,6);
②当△FED≌△ABC时,FE=AB=2,FD=AC=
,则
,
解得,
或
,
∴F3(5,5),F4(3,3);
综上所述,点F的坐标是:F1(2,8),F2(0,6),F3(5,5),F4(3,3).
故答案是:F1(2,8),F2(0,6),F3(5,5),F4(3,3).
 解:设点F的坐标是(x,y).
解:设点F的坐标是(x,y).∵A(1,2),B(3,2),C(4,3),D(2,6),E(3,5),
∴AB=2,BC=
| 2 |
| 10 |
| 2 |
①当△FDE≌△ABC时,FE=AC=
| 10 |
|
解得,
|
|
∴F1(2,8),F2(0,6);
②当△FED≌△ABC时,FE=AB=2,FD=AC=
| 10 |
|
解得,
|
|
∴F3(5,5),F4(3,3);
综上所述,点F的坐标是:F1(2,8),F2(0,6),F3(5,5),F4(3,3).
故答案是:F1(2,8),F2(0,6),F3(5,5),F4(3,3).
点评:本题考查了全等三角形的性质、坐标与图形性质.解答该题时,采用了“分类讨论”的数学思想,以防漏解.

练习册系列答案
相关题目
 (2006•厦门模拟)如图,AB是斜靠在墙壁上的固定爬梯,梯脚B到墙脚C的距离1.6m,梯上一点D到墙面的距离1.4m,BD长0.5m,则梯子的长为( )
(2006•厦门模拟)如图,AB是斜靠在墙壁上的固定爬梯,梯脚B到墙脚C的距离1.6m,梯上一点D到墙面的距离1.4m,BD长0.5m,则梯子的长为( ) (2006•厦门模拟)下列几个函数图象可能如图所示的是函数( )
(2006•厦门模拟)下列几个函数图象可能如图所示的是函数( )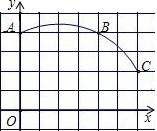 (2006•厦门模拟)如图,在平面直角坐标系中,一条圆弧经过正方形网格格点A,B,C,其中点B(4,4),则该圆弧所在圆的圆心坐标为
(2006•厦门模拟)如图,在平面直角坐标系中,一条圆弧经过正方形网格格点A,B,C,其中点B(4,4),则该圆弧所在圆的圆心坐标为