题目内容
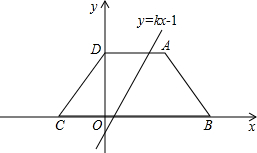 如图:等腰梯形ABCD中,AD∥BC,BC在x轴上,直线y=kx-1平分ABCD的面积,已知A(4,2),则k=________.
如图:等腰梯形ABCD中,AD∥BC,BC在x轴上,直线y=kx-1平分ABCD的面积,已知A(4,2),则k=________.
1
分析:首先过A作AE⊥BC于E,连接OA、DE交于点P,由四边形ABCD是等腰梯形,易证得Rt△COD≌Rt△BEA,即可得S△COD=S△BEA,又易证得四边形ADOE是矩形,由P为矩形ADOE的对称中心,则过P点的直线平分矩形ADOE的面积,可得一次函数y=kx-1的图象经过点P,又由A(4,2),可求得点P的坐标,继而求得答案.
解答: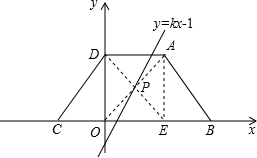 解:过A作AE⊥BC于E,连接OA、DE交于点P,
解:过A作AE⊥BC于E,连接OA、DE交于点P,
∵四边形ABCD是等腰梯形,
∴CD=AB,
∵∠COD=∠AEB=90°,
∴△COD和△BEA是直角三角形,
在Rt△COD和Rt△BEA中,
∵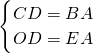 ,
,
∴Rt△COD≌Rt△BEA(HL),
∴S△COD=S△BEA,
∵AD∥BC,AE⊥BC,
∴AE∥OD,
∴四边形ADOE是矩形,
∴P为矩形ADOE的对称中心,则过P点的直线平分矩形ADOE的面积,
∵直线y=kx-1平分ABCD的面积,
∴一次函数y=kx-1的图象经过点P,
∵点A(4,2),O(0,0),
∴P点坐标为(2,1),
代入得:2k-1=1,
解得:k=1.
故答案为:1.
点评:此题考查了一次函数的性质、等腰梯形的性质、全等三角形的判定与性质以及矩形的判定与性质.此题难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.
分析:首先过A作AE⊥BC于E,连接OA、DE交于点P,由四边形ABCD是等腰梯形,易证得Rt△COD≌Rt△BEA,即可得S△COD=S△BEA,又易证得四边形ADOE是矩形,由P为矩形ADOE的对称中心,则过P点的直线平分矩形ADOE的面积,可得一次函数y=kx-1的图象经过点P,又由A(4,2),可求得点P的坐标,继而求得答案.
解答:
 解:过A作AE⊥BC于E,连接OA、DE交于点P,
解:过A作AE⊥BC于E,连接OA、DE交于点P,∵四边形ABCD是等腰梯形,
∴CD=AB,
∵∠COD=∠AEB=90°,
∴△COD和△BEA是直角三角形,
在Rt△COD和Rt△BEA中,
∵
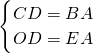 ,
,∴Rt△COD≌Rt△BEA(HL),
∴S△COD=S△BEA,
∵AD∥BC,AE⊥BC,
∴AE∥OD,
∴四边形ADOE是矩形,
∴P为矩形ADOE的对称中心,则过P点的直线平分矩形ADOE的面积,
∵直线y=kx-1平分ABCD的面积,
∴一次函数y=kx-1的图象经过点P,
∵点A(4,2),O(0,0),
∴P点坐标为(2,1),
代入得:2k-1=1,
解得:k=1.
故答案为:1.
点评:此题考查了一次函数的性质、等腰梯形的性质、全等三角形的判定与性质以及矩形的判定与性质.此题难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( )
14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( ) 24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.
24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC. (2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=
(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD= 如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm. 如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.