题目内容
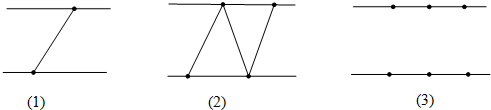
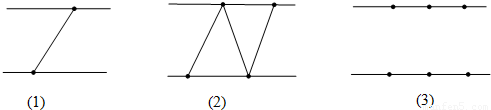
在下列图形中,各有一边长为4cm的正方形与一个8cm×2cm的长方形相重叠.问哪一个重叠的面积最大( )
A、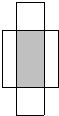 | B、 | C、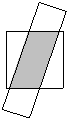 | D、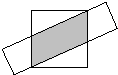 |
分析:A、阴影部分是长方形,所以长方形的面积等于长和宽的乘积;
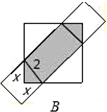
B、如图,设阴影部分等腰直角的腰为x,根据勾股定理求出x的值,所以,阴影部分的面积等于正方形的面积减去俩个空白三角形的面积;
C、图C,逆时针旋转90°从后面看,可与图D对比,因为图C阴影部分的倾斜度比图D阴影部分的倾斜度小,所以,图C中四边形的底比图D中四边形的底小,两图为等高不等底,所以图C阴影部分的面积小于图D阴影部分的面积;
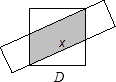
D、图D,设阴影部分平行四边形的底为x,根据正方形的面积=阴影部分的面积+两个空白三角形的面积,求出x的值,再得出阴影部分的面积;
图A、图C、图D中阴影部分四边形为等高不等底,因为倾斜度不同,所以图D中阴影部分的底最大,面积也就最大;因此,只要比较图B和图D阴影的面积大小,可得到图B阴影部分的面积最大.
B、如图,设阴影部分等腰直角的腰为x,根据勾股定理求出x的值,所以,阴影部分的面积等于正方形的面积减去俩个空白三角形的面积;
C、图C,逆时针旋转90°从后面看,可与图D对比,因为图C阴影部分的倾斜度比图D阴影部分的倾斜度小,所以,图C中四边形的底比图D中四边形的底小,两图为等高不等底,所以图C阴影部分的面积小于图D阴影部分的面积;
D、图D,设阴影部分平行四边形的底为x,根据正方形的面积=阴影部分的面积+两个空白三角形的面积,求出x的值,再得出阴影部分的面积;
图A、图C、图D中阴影部分四边形为等高不等底,因为倾斜度不同,所以图D中阴影部分的底最大,面积也就最大;因此,只要比较图B和图D阴影的面积大小,可得到图B阴影部分的面积最大.
解答:解:A、S阴影=2×4=8(cm2);
B、如图所示:根据勾股定理知,2x2=4,所以x=
,S阴影=4×4-2×
×(4-
)(4-
)=8
-2(cm2);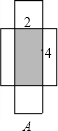
C、图C,逆时针旋转90°,并从后面看,可与图D对比,因为图C的倾斜度比图D的倾斜度小,所以,图C的底比图D的底小,两图为等高不等底,所以图C阴影部分的面积小于图D阴影部分的面积.
D、如图:设阴影部分平行四边形的底为x,所以,直角三角形的短直角边是
因为正方形的面积=阴影部分的面积+两个空白三角形的面积,
所以,
×4×
×2+2x=16,解得x=
,S阴影=2×
=
因为,
≈1.414,
≈2.646,所以,8
-2≈9.312,
≈8.775;
即8
-2>
,图B阴影的面积大于图D阴影的面积;
又因为图A、图C、图D中阴影部分四边形为等高不等底,因为图D阴影的倾斜度最大,所以图D中阴影部分的底最大;
故选B
B、如图所示:根据勾股定理知,2x2=4,所以x=
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |



C、图C,逆时针旋转90°,并从后面看,可与图D对比,因为图C的倾斜度比图D的倾斜度小,所以,图C的底比图D的底小,两图为等高不等底,所以图C阴影部分的面积小于图D阴影部分的面积.
D、如图:设阴影部分平行四边形的底为x,所以,直角三角形的短直角边是
| x2-16 |
因为正方形的面积=阴影部分的面积+两个空白三角形的面积,
所以,
| 1 |
| 2 |
| x2-16 |
8(
| ||
| 3 |
8(
| ||
| 3 |
16(
| ||
| 3 |
因为,
| 2 |
| 7 |
| 2 |
16(
| ||
| 3 |
即8
| 2 |
16(
| ||
| 3 |
又因为图A、图C、图D中阴影部分四边形为等高不等底,因为图D阴影的倾斜度最大,所以图D中阴影部分的底最大;
故选B
点评:本题考查了矩形、三角形面积的计算,找出图A、图B、图D阴影部分四边形等高不等底的特征,倾斜度越大的面积越大,是解答本题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 21、对某班学生一次数学测验成绩进行统计分析,各分数段的人数如图所示(分数取正整数),请认真观察图形,并回答下列问题.
21、对某班学生一次数学测验成绩进行统计分析,各分数段的人数如图所示(分数取正整数),请认真观察图形,并回答下列问题. 23、实验中学现有学生2870人,学校为了进一步丰富学生课余生活,拟调查各兴趣小组活动情况,为此校学生会委托小容、小易进行一次随机抽样调查.根据采集到的数据,小容绘制的统计图1,小易绘制的统计图2(不完整)如下:
23、实验中学现有学生2870人,学校为了进一步丰富学生课余生活,拟调查各兴趣小组活动情况,为此校学生会委托小容、小易进行一次随机抽样调查.根据采集到的数据,小容绘制的统计图1,小易绘制的统计图2(不完整)如下: