题目内容
 如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E,若AD=5,AB=6,BC=9.
如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E,若AD=5,AB=6,BC=9.(1)求DC的长;
(2)求证:四边形ABCE是平行四边形.
分析:(1)∵AD∥BC,∴AB=DC=6;
(2)可先证△CDE∽△BCD,求得DE=4,可得AE=9,∴AE
BC∴四边形ABCE是平行四边形.
(2)可先证△CDE∽△BCD,求得DE=4,可得AE=9,∴AE
| ∥ |
. |
解答:(1)解:∵AD∥BC
∴AB=DC
∴DC=AB=6(2分)
(2)证明:∵AD∥BC,
∴∠EDC=∠BCD
又∵PC与⊙O相切
∴∠ECD=∠DBC
∴△CDE∽△BCD(4分)
∴
=
∴DE=
=
=4(6分)
∴AE=AD+DE=5+4=9(7分)
∴AE
BC
∴四边形ABCE是平行四边形.(9分)
∴AB=DC
∴DC=AB=6(2分)
(2)证明:∵AD∥BC,
∴∠EDC=∠BCD
又∵PC与⊙O相切
∴∠ECD=∠DBC
∴△CDE∽△BCD(4分)
∴
| DC |
| BC |
| DE |
| DC |
∴DE=
| DC2 |
| BC |
| 62 |
| 9 |
∴AE=AD+DE=5+4=9(7分)
∴AE
| ∥ |
. |
∴四边形ABCE是平行四边形.(9分)
点评:此题主要考查平行四边形的判定,综合利用了切线和相似三角形的性质.

练习册系列答案
相关题目
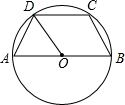 如图,梯形ABCD内接于⊙O,AB∥CD,AB为直径,DO平分∠ADC,则∠DAO的度数是( )
如图,梯形ABCD内接于⊙O,AB∥CD,AB为直径,DO平分∠ADC,则∠DAO的度数是( )| A、90° | B、80° | C、70° | D、60° |
 24、如图,梯形ABCD内接于⊙O,BC∥AD,AC与BD相交于点E,在不添加任何辅助线的情况下:
24、如图,梯形ABCD内接于⊙O,BC∥AD,AC与BD相交于点E,在不添加任何辅助线的情况下: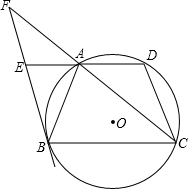 F.
F. 如图,梯形ABCD内接于⊙O,AD∥BC,∠DAB=49°,则∠AOC的度数为
如图,梯形ABCD内接于⊙O,AD∥BC,∠DAB=49°,则∠AOC的度数为