Question

如图所示，⊙O 的半径是4，PA、PB分别与⊙O相切于点A、点B，若PA与PB之间的夹角∠APB=60°，

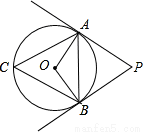
（1）若点C是圆上的一点，试求∠ACB的大小；

（2）求△ABP的周长

Answer 1

（1）60°或120°；（2）12．

【解析】

试题分析：（1）根据切线性质得出∠PAO=∠PBO=90°，求出∠AOB，根据圆周角定理求出即可；

（2）连接OP，求出△APB是等边三角形，∠APO=30°，求出OP，求出AP，即可求出答案．

试题解析：（1）∵PA、PB分别与⊙O相切于点A、点B，

∴∠PAO=∠PBO=90°，

∵∠APB=60°，

∴∠AOB=360°-90°-90°-60°=120°，

当C在优弧AB上时，∠ACB=∠AOB=60°，

当C在劣弧AB上时，∠ACB=180°-60°=120°；

（2）连接OP，

∵PA、PB分别与⊙O相切于点A、点B，∠APB=60°，

∴PA=PB，∠APO=∠APB=30°，

∴△APB是等边三角形，

∴PA=AB=PB，

∵∠PAO=90°，∠APO=30°，OA=4，

∴OP=2AO=8，由勾股定理得：AP=4，

∴△ABP的周长是AP+AB+BP=3×4=12．

考点：切线的性质．