题目内容
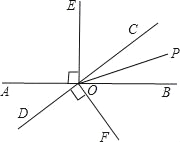
如图，直线AB与CD相交于点O，OE⊥AB，OF⊥CD，OP是∠BOC的平分线．
（1）请写出图中所有∠EOC的补角 ．
（2）如果∠POC：∠EOC=2：5．求∠BOF的度数．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
快乐小博士巩固与提高系列答案题目内容
如图，直线AB与CD相交于点O，OE⊥AB，OF⊥CD，OP是∠BOC的平分线．
（1）请写出图中所有∠EOC的补角 ．
（2）如果∠POC：∠EOC=2：5．求∠BOF的度数．
快乐小博士巩固与提高系列答案
）
B. 
C. 
D. 
的一根为
与
的解，则
的值是（ ）