题目内容
若f(x)表示自变量x相对应的函数值,且f(x)=
.关于x的方程f(x)=x+k有三个不相等的实数根,则k的取值范围是( )
|
分析:根据f(x)的函数表达式,①x≥0时,可得出关于x的一元二次方程,根据题意,可得方程应该有两个不相等的非负数根,②当x<0时,可得出关于x的一元一次方程,可得出方程有一个负数根,从而分别确定k的范围即可.
解答:解:①当x≥0时,方程f(x)=x+k,可化为:x2-4x+2=x+k,即x2-5x+2-k=0,
∵方程有两个不相等的非负数根,
∴
,
解得:-
<x≤2;
②当x<0时,方程f(x)=x+k,可化为:-2=x+k,即x=-2-k,
解得:k>-2;
综合①②可得-2<k≤2.
故选C.
∵方程有两个不相等的非负数根,
∴
|
解得:-
| 17 |
| 4 |
②当x<0时,方程f(x)=x+k,可化为:-2=x+k,即x=-2-k,
解得:k>-2;
综合①②可得-2<k≤2.
故选C.
点评:此题考查了分段函数及一元二次方程的根与系数的关系,题目出的新颖,解答此类题目关键是看清要使方程有3个根,需要各个方程满足什么条件,有一定难度.

练习册系列答案
相关题目
 已知函数y=x2+bx+c(x≥0),满足当x=1时,y=-1,且当x=0与x=4时的函数值相等.
已知函数y=x2+bx+c(x≥0),满足当x=1时,y=-1,且当x=0与x=4时的函数值相等. 已知函数y=x2+bx+c(x≥0),满足当x=1时,y=-1,且当x=0与x=4时的函数值相等.
已知函数y=x2+bx+c(x≥0),满足当x=1时,y=-1,且当x=0与x=4时的函数值相等.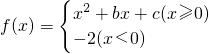 又已知关于x的方程f(x)=x+k有三个不相等的实数根,请利用图象直接写出实数k的取值范围.
又已知关于x的方程f(x)=x+k有三个不相等的实数根,请利用图象直接写出实数k的取值范围. 又已知关于x的方程f(x)=x+k有三个不相等的实数根,请利用图象直接写出实数k的取值范围.
又已知关于x的方程f(x)=x+k有三个不相等的实数根,请利用图象直接写出实数k的取值范围.
 又已知关于x的方程f(x)=x+k有三个不相等的实数根,请利用图象直接写出实数k的取值范围.
又已知关于x的方程f(x)=x+k有三个不相等的实数根,请利用图象直接写出实数k的取值范围.