题目内容
有一等腰直角三角形纸片，以它的对称轴为折痕，将三角形对折，得到的三角形还是等腰直角三角形（如图）．依照上述方法将原等腰直角三角形折叠四次，所得小等腰直角三角形的周长是原等腰直角三角形周长的________倍．
分析：根据折叠的性质可知折叠一次后得到的等腰直角三角形与原等腰直角三角形是相似三角形，再根据相似比求面积比．
解答：由于折叠一次后得到的等腰直角三角形与原等腰直角三角形是相似三角形，
得到的相似比=现在的斜边：原来的斜边=
，∴折叠四次，所得小等腰直角三角形的周长是原等腰直角三角形周长的（
）4=倍．故答案为：
．点评：本题考查了翻折变换、等腰直角三角形及相似三角形的判定与性质，属于规律型题目，解答本题需要得出折叠前后的相似比，有一定的难度．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
cm，∠ACB=90°现要沿AB边向上依次截取宽度均为2cm的长方形纸条,如图所示.已知截得的长方形纸片中有一块是正方形,则这块正方形纸片是（ ）
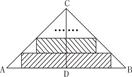
如图，在每个小正方形的边长均为1个单位长度的方格纸中，有一条线段AB，点A、B均与小正方形的顶点重合．