题目内容
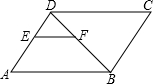
 如图,E是平行四边形ABCD的边BC上一点,AE交BD于F,G为BD上一点,且∠1=∠2,则图中相似三角形(全等除外)的对数为
如图,E是平行四边形ABCD的边BC上一点,AE交BD于F,G为BD上一点,且∠1=∠2,则图中相似三角形(全等除外)的对数为
- A.2对
- B.3对
- C.4对
- D.5对
B
分析:由平行四边形的性质,结合相似三角形的判定定理“两角法”进行解答.
解答: 解:①如图,∠1=∠2,∠BEF=∠AGF,则△BEF∽△AGF;
解:①如图,∠1=∠2,∠BEF=∠AGF,则△BEF∽△AGF;
②如图,在平行四边形ABCD中,∠2=∠3,又∠BEF=∠DAF,则△BEF∽△DAF;
③∵△BEF∽△AGF,△BEF∽△DAF,∴△AGF∽△DAF;
综上所述,图中相似三角形(全等除外)的对数为3对.
故选B.
点评:本题考查了相似三角形的判定,平行四边形的性质.两角法:有两组角对应相等的两个三角形相似.
分析:由平行四边形的性质,结合相似三角形的判定定理“两角法”进行解答.
解答:
 解:①如图,∠1=∠2,∠BEF=∠AGF,则△BEF∽△AGF;
解:①如图,∠1=∠2,∠BEF=∠AGF,则△BEF∽△AGF;②如图,在平行四边形ABCD中,∠2=∠3,又∠BEF=∠DAF,则△BEF∽△DAF;
③∵△BEF∽△AGF,△BEF∽△DAF,∴△AGF∽△DAF;
综上所述,图中相似三角形(全等除外)的对数为3对.
故选B.
点评:本题考查了相似三角形的判定,平行四边形的性质.两角法:有两组角对应相等的两个三角形相似.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 如图,E是平行四边形ABCD的AD边上一点,过点E作EF∥AB交BD于F,若DE:EA=2:3,EF=4,则CD的长为( )
如图,E是平行四边形ABCD的AD边上一点,过点E作EF∥AB交BD于F,若DE:EA=2:3,EF=4,则CD的长为( )A、
| ||
| B、8 | ||
| C、10 | ||
| D、16 |
 22、如图,E是平行四边形ABCD的边BA延长线上一点,连接EC,交AD于F.
22、如图,E是平行四边形ABCD的边BA延长线上一点,连接EC,交AD于F. (2012•黄埔区一模)如图,AC是平行四边形ABCD的对角线,∠ACB=∠ACD.
(2012•黄埔区一模)如图,AC是平行四边形ABCD的对角线,∠ACB=∠ACD. (2012•荆州模拟)如图,G是平行四边形ABCD的边CD延长线上一点,BG交AC于E,交AD于F,则图中与△FGD相似的三角形有( )
(2012•荆州模拟)如图,G是平行四边形ABCD的边CD延长线上一点,BG交AC于E,交AD于F,则图中与△FGD相似的三角形有( ) 如图,ABCD是平行四边形,∠DAB=α,AC是对角线.△ADC绕点A旋转β度角,得到△AD′C′,连结D′B.若△ABC≌△BAD′,试求出α与β的关系.
如图,ABCD是平行四边形,∠DAB=α,AC是对角线.△ADC绕点A旋转β度角,得到△AD′C′,连结D′B.若△ABC≌△BAD′,试求出α与β的关系.