题目内容
如图,抛物线y=x2-2mx+(m+1)2(m>0)的顶点为A,另一条抛物线y=ax2+n(a<0)的顶点为B,与 x轴正半轴交于点C,已知点P(1,3)在线段AB上(点P与点A、B不重合).
x轴正半轴交于点C,已知点P(1,3)在线段AB上(点P与点A、B不重合).
(1)求顶点B的坐标;
(2)当点P恰好为AB的中点,且由A、B、C三点构成的三角形为等腰三角形时,求a的值?
解:(1)∵y=x2-2mx+(m+1)2(m>0),
∴y=(x-m)2+2m+1,
∴顶点A的坐标是(m,2m+1),
设直线AB的解析式是y=kx+b,
∵直线过A、P,把A、P的坐标代入得: ,
,
∵m≠1,
∴k=2,b=1,
∴直线AB的解析式是y=2x+1,
∴B的坐标是(0,1),
答:顶点B的坐标是(0,1).
(2)解:设C的坐标是(x,0),
当点P恰好是AB的中点时,可得A的坐标是(2,5),
∵B的坐标是(0,1),
∴n=1,
即y=ax2+1,
当△ABC是等腰三角形时,分以下三种情况:
①若AB=AC=2 ,
,
∵AC2=(x-2)2+25,不成立舍去,
②若AB=BC=2 ,
,
∵BC2=1+x2,
∵x>0,
∴x= ,
,
∴C的坐标是( ,0),
,0),
代入y=ax2+1(a<0)得:a=-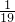 ,
,
③若AC=BC,
∵AC2=BC2,
(x-2)2+25=1+x2,
∵x>0,
∴x=7,
∴C的坐标是(7,0),
代入求出a=-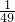 ,
,
综合上述满足条件的a有-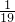 、-
、-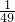 两个,
两个,
答:a的值是-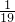 ,-
,-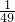 .
.
分析:(1)设直线AB的解析式是y=kx+b,把A、P的坐标代入k和b,即可求出答案;
(2)设C的坐标是(x,0),当点P恰好是AB的中点时求出A的坐标和n,得出y=ax2+1,分三种情况①若AB=AC=2 ,②若AB=BC=2
,②若AB=BC=2 ,③若AC=BC,根据勾股定理求出x,得出C的坐标,代入解析式即可求出a.
,③若AC=BC,根据勾股定理求出x,得出C的坐标,代入解析式即可求出a.
点评:本题主要考查对二次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,勾股定理,等腰三角形的性质,解二元一次方程组等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.
∴y=(x-m)2+2m+1,
∴顶点A的坐标是(m,2m+1),
设直线AB的解析式是y=kx+b,
∵直线过A、P,把A、P的坐标代入得:
 ,
,∵m≠1,
∴k=2,b=1,
∴直线AB的解析式是y=2x+1,
∴B的坐标是(0,1),
答:顶点B的坐标是(0,1).
(2)解:设C的坐标是(x,0),
当点P恰好是AB的中点时,可得A的坐标是(2,5),
∵B的坐标是(0,1),
∴n=1,
即y=ax2+1,
当△ABC是等腰三角形时,分以下三种情况:
①若AB=AC=2
 ,
,∵AC2=(x-2)2+25,不成立舍去,
②若AB=BC=2
 ,
,∵BC2=1+x2,
∵x>0,
∴x=
 ,
,∴C的坐标是(
 ,0),
,0),代入y=ax2+1(a<0)得:a=-
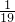 ,
,③若AC=BC,
∵AC2=BC2,
(x-2)2+25=1+x2,
∵x>0,
∴x=7,
∴C的坐标是(7,0),
代入求出a=-
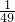 ,
,综合上述满足条件的a有-
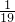 、-
、-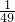 两个,
两个,答:a的值是-
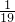 ,-
,-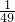 .
.分析:(1)设直线AB的解析式是y=kx+b,把A、P的坐标代入k和b,即可求出答案;
(2)设C的坐标是(x,0),当点P恰好是AB的中点时求出A的坐标和n,得出y=ax2+1,分三种情况①若AB=AC=2
 ,②若AB=BC=2
,②若AB=BC=2 ,③若AC=BC,根据勾股定理求出x,得出C的坐标,代入解析式即可求出a.
,③若AC=BC,根据勾股定理求出x,得出C的坐标,代入解析式即可求出a.点评:本题主要考查对二次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,勾股定理,等腰三角形的性质,解二元一次方程组等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
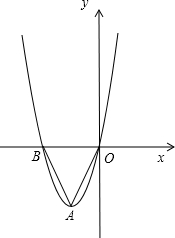 如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO.
如图,抛物线y=x2+4x与x轴分别相交于点B、O,它的顶点为A,连接AB,AO. 16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y
16、如图,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y 已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l.
已知如图,抛物线y=x2+(k2+1)x+k+1的对称轴是直线x=-1,且顶点在x轴上方.设M是直线x=-1左侧抛物线上的一动点,过点M作x轴的垂线MG,垂足为G,过点M作直线x=-1的垂线MN,垂足为N,直线x=-1与x轴的交于H点,若M点的横坐标为x,矩形MNHG的周长为l. (2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.
(2013•扬州)如图,抛物线y=x2-2x-8交y轴于点A,交x轴正半轴于点B.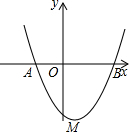 如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.
如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.