题目内容
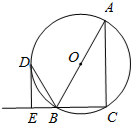 已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于D,DE∥AC交CB的延长线于E.
已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于D,DE∥AC交CB的延长线于E.(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若∠A=30°,BD=2cm,求
 |
| BD |
考点:切线的判定,弧长的计算
专题:
分析:(1)连接OD,由OB=OD,得出∠ODB=∠OBD,根据BD是△ABC的外角平分线,推出∠ODB=∠DBE,得到OD∥BE.推出BE⊥DE,根据AB是⊙O的直径,得到AC⊥CE,根据DE∥AC,即可推出OD⊥DE,从而证得直线DE与⊙O相切.
(2)由∠A=30°,根据三角形的外角性质求出∠DBE,进而求出∠DOB=60°,根据弧长公式即可求出弧BD的长.
(2)由∠A=30°,根据三角形的外角性质求出∠DBE,进而求出∠DOB=60°,根据弧长公式即可求出弧BD的长.
解答: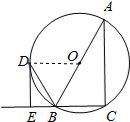 解:(1)直线DE与⊙O相切.
解:(1)直线DE与⊙O相切.
理由如下:连接OD,
∵OB=OD,
∴∠ODB=∠OBD.
∵BD是△ABC的外角平分线,
∴∠DBE=∠OBD.
∴∠DBE=∠ODB,
∴BE∥OD.
∵AB是⊙O的直径,
∴∠C=90°.
∵DE∥AC,
∴∠DEB=90°,
∴OD⊥DE且点D在⊙O上.
∴直线DE与⊙O相切.
(2)∵∠A=30°,
∴∠ABC=60°,
∴∠DBO=∠DBE=60°,
∵BE∥OD,
∴∠DOB=60°,
∵BD=2cm,
∴OB=OD=2,
∴
=
π.
 解:(1)直线DE与⊙O相切.
解:(1)直线DE与⊙O相切.理由如下:连接OD,
∵OB=OD,
∴∠ODB=∠OBD.
∵BD是△ABC的外角平分线,
∴∠DBE=∠OBD.
∴∠DBE=∠ODB,
∴BE∥OD.
∵AB是⊙O的直径,
∴∠C=90°.
∵DE∥AC,
∴∠DEB=90°,
∴OD⊥DE且点D在⊙O上.
∴直线DE与⊙O相切.
(2)∵∠A=30°,
∴∠ABC=60°,
∴∠DBO=∠DBE=60°,
∵BE∥OD,
∴∠DOB=60°,
∵BD=2cm,
∴OB=OD=2,
∴
 |
| BD |
| 2 |
| 3 |
点评:本题主要考查对切线的性质,三角形的外角性质,三角形的角平分线,平行线的判定,圆周角定理,弧长公式,等腰三角形的性质等知识点的理解和掌握,综合运用这些性质进行推理是证此题的关键.

练习册系列答案
相关题目
一个整式减去3m,结果等于5m2-3m-5.这个整式是( )
| A、5m2-5 |
| B、5m2-6m-5 |
| C、5m2+5 |
| D、-5m-6m+5 |
抛物线y=-8x2+5可以看作是由y=-8x2按下列何种变换得到的( )
| A、向上平移5个单位 |
| B、向下平移5个单位 |
| C、向左平移5个单位 |
| D、向右平移5个单位 |