题目内容
已知,如图:在Rt△ABC中,∠C=900,以BC为直径作⊙O交AB于D,取AC中点E,连结OE,ED的延长线与CB的延长线交于F.
(1)求证:DE是⊙O的切线:
(2)如果⊙O的半径为3cm,ED=4cm,求sin∠F的值.

(1)如图,连结OD,∴OD=OC=OB,
∴∠OBD=∠ODB,又∵E为AC的中点, O是CB的中点,
所以OE∥AB,
∴∠COE=∠CBA,∠EOD=∠ODB,∴∠COE=∠EOD,
又∵OE=OE,所以△OCE与△ODE
全等,所以∠ODB=∠OCE=90°
即ED⊥OD,所以DE是圆O的切线.
(2)如图,由OC=OD=OB=3cm,
 ED=EC=4cm,
ED=EC=4cm,
∵∠F=∠F,∠FCE=∠FDO,
∴△FDO与△FCE相似,![]()
设FD=x,∴![]() ∴
∴![]()
∴![]()
![]()

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
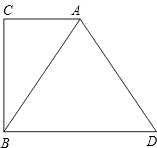 已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由.
已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由. (1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.
(1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD. (2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.
(2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE. 已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y. 已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.
已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.