题目内容
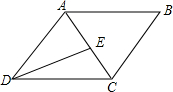 如图,已知E是平行四边形ABCD对角线AC上的点,连接DE.
如图,已知E是平行四边形ABCD对角线AC上的点,连接DE.(1)过点B在平行四边形内部作射线BF交AC于点F,且使∠CBF=∠ADE(要求:用尺规作图,保留作图痕迹,不写作法与证明)
(2)连接BE,DF,判断四边形BFDE的形状并证明.
分析:(1)作∠CBM=∠ADE,其中BM交CD于F即可;
(2)四边形BFDE的形状是平行四边形,连BE、DF,由于△ADE≌△CBF,根据全等三角形的性质得到DE=BF,∠AED=∠BFC,根据等角的补角相等可得∠DEF=∠BFE,则DE∥BF,根据平行四边形的判定即可得到结论.
(2)四边形BFDE的形状是平行四边形,连BE、DF,由于△ADE≌△CBF,根据全等三角形的性质得到DE=BF,∠AED=∠BFC,根据等角的补角相等可得∠DEF=∠BFE,则DE∥BF,根据平行四边形的判定即可得到结论.
解答:解:(1) 如图所示:
如图所示:
(2)四边形BFDE的形状是平行四边形,
理由如下:
∵在平行四边形ABCD中,∴∠A=∠C,AD=BC,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(ASA),
∴DE=BF,∠AED=∠BFC,
∵∠DEF=180°-∠AED,∠BFE=180°-∠BFC,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形DEBF是平行四边形.
 如图所示:
如图所示:(2)四边形BFDE的形状是平行四边形,
理由如下:
∵在平行四边形ABCD中,∴∠A=∠C,AD=BC,
在△ADE和△CBF中,
|
∴△ADE≌△CBF(ASA),
∴DE=BF,∠AED=∠BFC,
∵∠DEF=180°-∠AED,∠BFE=180°-∠BFC,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形DEBF是平行四边形.
点评:综合考查了角的作图,平行四边形的性质和全等三角形的判定的知识,三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 19、如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论:
19、如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论: 如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(6,0)和C(0,4 )三个点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(6,0)和C(0,4 )三个点. 如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=2AD,DC⊥l4,则四边形ABCD的面积是
如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=2AD,DC⊥l4,则四边形ABCD的面积是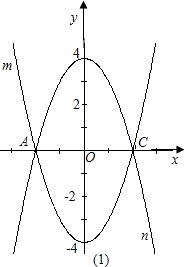

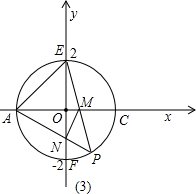
 如图,已知直l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是2,如果正方形ABCD的四个顶点分别在四条直线上,则正方形边长的值为
如图,已知直l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是2,如果正方形ABCD的四个顶点分别在四条直线上,则正方形边长的值为