题目内容
在同一坐标系中,函数y=k1x(k1≠0)的图象与y=
(k2≠0)的图象没有公共点,则k1k2
| k2 | x |
<
<
0.(填入“>”或“<”号)分析:若直线y=k1x(k1≠0)的图象与y=
(k2≠0)的图象没有公共点,就是说k1x=
无解.
| k2 |
| x |
| k2 |
| x |
解答:解:依题意可得,k1x=
无解,
即x2=
无解,
则
<0,
即k1和k2异号,
所以k1k2<0.
故答案为<.
| k2 |
| x |
即x2=
| k2 |
| k1 |
则
| k2 |
| k1 |
即k1和k2异号,
所以k1k2<0.
故答案为<.
点评:本题综合考查反比例函数与方程组的相关知识点,难度不大,主要掌握任何一个数的平方都大于或等于0,小于0就无解.

练习册系列答案
相关题目
在同一坐标系中画函数y=
和y=-kx+3的图象,大致图形可能是( )
| k |
| x |
A、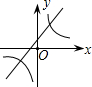 |
B、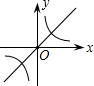 |
C、 |
D、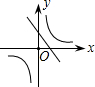 |