��Ŀ����
�ס�����λͬѧ��������Ϸ�����˼ס��������ڴ������мڴ��з��б��Ϊ1��2��3��4��5��5�����ҿڴ��з��б��Ϊ1��2��3��4��4������Ϸ���״Ӽڴ���һ���Ҵ��ҿڴ���һ��������������������֮�������-�����֣�����0ʱ��ʤ��С��0ʱ��ʤ������0ʱƽ�֣�����Ϊ�����Ϸ�����˫����ƽ����˵�����ɣ�������ƽ������Ա���Ϸ���һ����˫������ƽ����Ϸ����
�⣺��Ϸ����ƽ������Ϊ��
�б��ã�
���еȿ��ܵ������20�֣�����������������������֮�������-�����֣�����0�������10�У�����0�������4�֣�С��0�������6�֣�
��P��ʤ=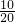 =
= ��P�һ�ʤ=
��P�һ�ʤ=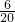 =
= ��
��
�� ��
�� ��
��
����Ϸ����ƽ��
��ʹ��Ϸ��ƽ���Ĺ���Ϊ����������������������֮��Ϊż������ʤ��֮��Ϊ�������һ�ʤ��
��������Ϸ����ƽ������Ϊ���г����ó����еȿ��ܵ���������ҳ�����֮�����0������0�Լ�С��0ʱ��������������������ʤ�ĸ��ʣ������жϲ���ƽ����Ҫʹ��Ϸ��ƽ���Ĺ��ɣ�
���������⿼������Ϸ�Ĺ�ƽ�ԣ��Լ��б�������״ͼ�����ж���Ϸ��ƽ�Ծ�Ҫ����ÿ���¼��ĸ��ʣ�������Ⱦ�ƽ������Ͳ���ƽ��
�б��ã�
| 1 | 2 | 3 | 4 | 5 | |
| 1 | ��1��1�� | ��2��1�� | ��3��1�� | ��4��1�� | ��5��1�� |
| 2 | ��1��2�� | ��2��2�� | ��3��2�� | ��4��2�� | ��5��2�� |
| 3 | ��1��3�� | ��2��3�� | ��3��3�� | ��4��3�� | ��5��3�� |
| 4 | ��1��4�� | ��2��4�� | ��3��4�� | ��4��4�� | ��5��4�� |
��P��ʤ=
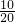 =
= ��P�һ�ʤ=
��P�һ�ʤ=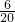 =
= ��
����
 ��
�� ��
������Ϸ����ƽ��
��ʹ��Ϸ��ƽ���Ĺ���Ϊ����������������������֮��Ϊż������ʤ��֮��Ϊ�������һ�ʤ��
��������Ϸ����ƽ������Ϊ���г����ó����еȿ��ܵ���������ҳ�����֮�����0������0�Լ�С��0ʱ��������������������ʤ�ĸ��ʣ������жϲ���ƽ����Ҫʹ��Ϸ��ƽ���Ĺ��ɣ�
���������⿼������Ϸ�Ĺ�ƽ�ԣ��Լ��б�������״ͼ�����ж���Ϸ��ƽ�Ծ�Ҫ����ÿ���¼��ĸ��ʣ�������Ⱦ�ƽ������Ͳ���ƽ��

��ϰ��ϵ�д�
 ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
�����Ŀ