题目内容
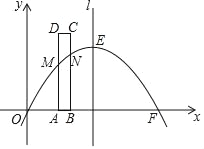
【题目】如图,直线![]() 与
与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与反比例函数
,与反比例函数![]() 图象交于点
图象交于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴的垂线交该反比例函数图象于点
轴的垂线交该反比例函数图象于点![]() .
.
![]() 求点
求点![]() 的坐标.
的坐标.
![]() 若
若![]() .
.
①求![]() 的值.
的值.
②试判断点![]() 与点
与点![]() 是否关于原点
是否关于原点![]() 成中心对称?并说明理由.
成中心对称?并说明理由.
【答案】![]() 点
点![]() 的坐标为
的坐标为![]() ;②点
;②点![]() 与点
与点![]() 关于原点
关于原点![]() 成中心对称.理由见解析.
成中心对称.理由见解析.
【解析】
(1)令一次函数中y=0,解关于x的一元一次方程,即可得出结论;
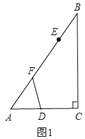
(2)①过点C作CF⊥x轴于点F,设AE=AC=t,由此表示出点E的坐标,利用特殊角的三角形函数值,通过计算可得出点C的坐标,再根据反比例函数图象上点的坐标特征可得出关于t的一元二次方程,解方程即可得出结论;
②根据点在直线上设出点D的坐标,根据反比例函数图象上点的坐标特征可得出关于点D横坐标的一元二次方程,解方程即可得出点D的坐标,结合①中点E的坐标即可得出结论.
![]() 当
当![]() 时,得
时,得![]() ,解得:
,解得:![]() .
.
∴点![]() 的坐标为
的坐标为![]() .:
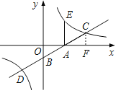
.:![]() ①过点
①过点![]() 作
作![]() 轴于点
轴于点![]() ,如图所示.
,如图所示.
设![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
B(0,![]() )∴AB=3
)∴AB=3
∵![]()
∴![]()
∴![]() ,
,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() .
.
∴![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
∴![]() .
.
②点![]() 与点
与点![]() 关于原点
关于原点![]() 成中心对称,理由如下:
成中心对称,理由如下:
设点![]() 的坐标是
的坐标是![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() .
.
又∵点![]() 的坐标为
的坐标为![]() ,
,
∴点![]() 与点
与点![]() 关于原点
关于原点![]() 成中心对称.
成中心对称.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目