题目内容
如图，有八个全等的直角三角形拼成一个大四边形ABCD和中间一个小四边形MNPQ，连接EF、GH得到四边形EFGH，设S四边形ABCD=S1，S四边形EFGH=S2，S四边形MNPQ=S3，若S1+S2+S3=20，则S2= .
【答案】
【解析】
试题分析：根据图形的特征设出四边形MNPQ的面积设为x，将其余八个全等的三角形面积一个设为y，从而用x，y表示出S1，S2，S3，得出答案即可．
将四边形MNPQ的面积设为x，将其余八个全等的三角形面积一个设为y，
∵S四边形ABCD=S1，S四边形EFGH=S2，S四边形MNPQ=S3，若S1+S2+S3=20，
∴得出S1=8y+x，S2=4y+x，S3=x，
∴S1+S2+S3=3x+12y=20，
故3x+12y=20，
∴x+4y=
S2=x+4y=
考点：1.平行四边形的判定与性质；2.全等三角形的性质．
练习册系列答案
阅读快车系列答案
相关题目
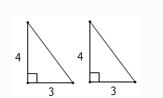29、如图，有两个全等的直角三角形，它们的边长分别为3和4，把这两个直角三角形拼成一个三角形或一个四边形，在这些图形中，周长最小值是
如图，有八个全等的直角三角形拼成一个大四边形ABCD和中间一个小四边形MNPQ，连接EF、GH得到四边形EFGH，设S四边形ABCD=S1，S四边形EFGH=S2，S四边形MNPQ=S3，若S1+S2+S3=
如图，有八个全等的直角三角形拼成一个大四边形ABCD和中间一个小四边形MNPQ，连接EF、GH得到四边形EFGH，设S四边形ABCD=S1，S四边形EFGH=S2，S四边形MNPQ=S3，若S1+S2+S3=
，则S2=________．