题目内容
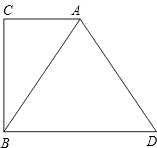
 已知:如图,在RT△ABC中,∠C=90°,∠ABC=45°D是BC上的点,BD=10.∠ADC=60°.求AC(
已知:如图,在RT△ABC中,∠C=90°,∠ABC=45°D是BC上的点,BD=10.∠ADC=60°.求AC( ≈1.73,结果保留整数).
≈1.73,结果保留整数).
解:在Rt△ACD中,∠C=90°,∠ADC=60°,
tan60°= =
=
设CD=x,
∴AC= x(2分)
x(2分)
在Rt△ACB中,∠C=90°,∠ABC=45°
∴AC=BC,BD=10
∴ x=x+10(4分)
x=x+10(4分)
解得:x= ≈14,
≈14,
即AC约14米(6分)
分析:首先在直角三角形ACD中,利用30°直角三角形的性质求得CD的长,再进一步根据勾股定理求得AC的长.
点评:本题考查了锐角三角函数的定义及特殊角的三角函数值,属于基础题.
tan60°=
 =
=
设CD=x,
∴AC=
 x(2分)
x(2分)在Rt△ACB中,∠C=90°,∠ABC=45°
∴AC=BC,BD=10
∴
 x=x+10(4分)
x=x+10(4分)解得:x=
 ≈14,
≈14,即AC约14米(6分)
分析:首先在直角三角形ACD中,利用30°直角三角形的性质求得CD的长,再进一步根据勾股定理求得AC的长.
点评:本题考查了锐角三角函数的定义及特殊角的三角函数值,属于基础题.

练习册系列答案
相关题目
 已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由.
已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由. (1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.
(1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD. (2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.
(2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE. 已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y. 已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.
已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.