Question

如图，已知直线y=mx+n交x轴于A，交y轴于b，且∠BAO=30°，P为上一点，PE⊥y轴于E，PF⊥x轴于F，分别交AB于M，N，若AM•BN=，则k=________．

Answer 1

分析：过M作MQ垂直于x轴，过N作ND垂直于y轴，由三个角为直角的四边形为矩形得到四边形PEDN与PFQM为矩形，利用矩形的对边相等得到MQ=PF，DN=PE，设P（a，b），即PE=a，PF=b，在直角三角形AMQ中，利用30度角所对的直角边等于斜边的一半得到AM=2PF=2b，在直角三角形BDN中，利用锐角三角形函数定义表示出BN，由AM•BN=列出关系式，求出ab的值，将P坐标代入反比例解析式中得到k=ab，即可得出k的值．
解答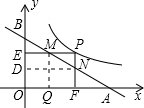：解：过M作MQ⊥x轴，过N作ND⊥y轴，
可得：四边形MQFP与四边形PEDN为矩形，
设P（a，b），
∴MQ=PF=b，DN=PE=a，
在Rt△AMQ中，∠BAO=30°，
∴MQ=PF=AM，即AM=2PF=2b，
在Rt△BDN中，∠OBA=60°，
∴sin60°===，
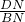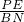∴BN=PE=a，
又AM•BN=，
∴2PF•PE=，即PE•PF=ab=，
则k=ab=．
故答案为：
点评：此题属于反比例函数综合题，涉及的知识有：反比例函数k的几何意义，锐角三角函数定义，含30°直角三角形的性质，坐标与图形性质，以及矩形的判定与性质，本题的突破点是作出辅助线MQ⊥x轴，ND⊥y轴．