题目内容

请写出一个解为1和3的一元二次方程：________．

x2-4x+3=0
分析：根据题意可设方程为：x2+bx+c=0，两根分别为x1，x2，则由根与系数关系可得：x1+x2=-b，x1x2=c，分别代入即可得到满足条件的一个方程．
解答：根据题意可设方程为：x2+bx+c=0，两根分别为x1，x2，
则由根与系数关系可得：x1+x2=-b，x1x2=c，
又由题意知，x1=1，x2=3，
可解得：b=-4，c=3，
∴满足条件的一个方程为：x2-4x+3=0；
点评：本题比较简单，主要考查一元二次方程的根与系数的关系，只要熟悉根与系数的关系，就很容易写出正确的结果．
练习册系列答案
相关题目
在课外小组活动时，小慧拿来一道题（原问题）和小东、小明交流．
原问题：如图1，已知△ABC，∠ACB=90°，∠ABC=45°，分别以AB、BC为边向外作△ABD与△BCE，且DA=DB，EB=EC，∠ADB=∠BEC=90°，连接DE交AB于点F．探究线段DF与EF的数量关系．
小慧同学的思路是：过点D作DG⊥AB于G，构造全等三角形，通过推理使问题得解．
小东同学说：我做过一道类似的题目，不同的是∠ABC=30°，∠ADB=∠BEC=60度．
小明同学经过合情推理，提出一个猜想，我们可以把问题推广到一般情况．
请你参考小慧同学的思路，探究并解决这三位同学提出的问题：
（1）写出原问题中DF与EF的数量关系；
（2）如图2，若∠ABC=30°，∠ADB=∠BEC=60°，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明；
（3）如图3，若∠ADB=∠BEC=2∠ABC，原问题中的其他条件不变，精英家教网你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明．
在“乌鲁木齐靓起来”的活动中，某社区决定利用9000盆菊花和8100盆太阳花搭配A，B两种园艺造型共100个摆放在社区．搭配每种园艺造型所需的花卉情况如下表所示：
   需要菊花（盆） 需要太阳花（盆） 
一个A造型   100  60
 一个B造型  80  100
综合上述信息，设搭配A种园艺造型x个，解答下列问题：
（1）请写出满足题意的不等式组，并求出其解集；
（2）若搭配一个A种园艺造型的成本为600元，搭配一个B种园艺造型的成本为800元，试确定搭配A种造型多少个时，可使这100个园艺造型的成本最低．
2010年11月12日至27日广州成功举办了第16届亚运会，当时广州亚组委提出“让广州靓起来”的口号，在“让广州靓起来”的活动中，广州市某社区决定利用9000盆菊花和8100盆太阳花搭配A，B两种园艺造型共100个摆放在社区．搭配每种园艺造型所需的花卉情况如下表所示：
需要菊花（盆） 需要太阳花（盆）
一个A造型 100 60
一个B造型 80 100
综合上述信息，设搭配A种园艺造型x个，解答下列问题：
（1）请写出满足题意的不等式组，并求出其解集；
（2）若搭配一个A种园艺造型的成本为600元，搭配一个B种园艺造型的成本为800元，试确定搭配A种造型多少个时，可使这100个园艺造型的成本最低？
14、请写出一个解为1和3的一元二次方程：
x2-4x+3=0
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

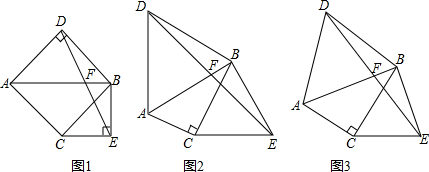精英家教网