Question

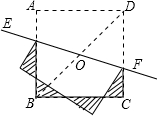（2013•保定二模）如图，已知正方形ABCD的对角线长为2

2

，点O为正方形的对称中心，将正方形ABCD沿过点O的直线EF折叠，则图中阴影部分四个三角形周长的和为

8

．

Answer 1

分析：先设正方形的边长为a，再根据对角线长为2

2

求出a的值，由图形翻折变换的性质可知AD=A′B′，A′H=AH，B′G=DG，由阴影部分的周长=A′B′+A′H+BH+BC+CG+B′G即可得出结论．

解答：解：设正方形的边长为a，则2a²=（2

2

）²，
解得：a=2，
翻折变换的性质可知AD=A′B′，A′H=AH，B′G=DG，
阴影部分的周长=A′B′+（A′H+BH）+BC+（CG+B′G）=AD+AB+BC+CD=2×4=8．
故答案为：8．

点评：本题考查的是翻折变换的性质，即折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．