题目内容
【题目】如图,∠ABD和∠BDC的平分线交于点E,BE的延长线交CD于点F,且∠1+∠2=90°.猜想∠2与∠3的关系并证明.
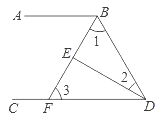
【答案】∠2+∠3=90°;证明见解析.
【解析】
试题分析:根据角平分线定义得出∠ABF=∠1,∠ABD=2∠1,∠BDC=2∠2,求出∠ABF+∠2=90°,∠ABD+∠BDC=180°,根据平行线的判定得出AB∥DC,根据平行线的性质得出∠3=∠ABF,即可得出答案.
试题解析:∠2+∠3=90°,
证明:∵∠ABD和∠BDC的平分线交于点E,
∴∠ABF=∠1,∠ABD=2∠1,∠BDC=2∠2,
∵∠1+∠2=90°,
∴∠ABF+∠2=90°,∠ABD+∠BDC=2×90°=180°,
∴AB∥DC,
∴∠3=∠ABF,
∴∠2+∠3=90°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】在作二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象时,先列出下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y1 | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 | … |
y2 | … | 0 | 2 | 4 | 6 | 8 | 10 | 12 | … |
请你根据表格信息回答下列问题,
(1)二次函数y1=ax2+bx+c的图象与y轴交点坐标为 ;
(2)当y1>y2时,自变量x的取值范围是 ;
(3)请写出二次函数y1=ax2+bx+c的三条不同的性质.