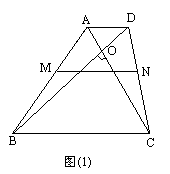
题目内容
 梯形ABCD中,对角线AC、BD相交于点O,过O点的直线分别交上、下底于E、F,则在图中与OE:OF的比值相等的线段比有
梯形ABCD中,对角线AC、BD相交于点O,过O点的直线分别交上、下底于E、F,则在图中与OE:OF的比值相等的线段比有
- A.4个
- B.5个
- C.7个
- D.8个
B
分析:由梯形ABCD中,AB∥CD,根据平行线分线段成比例定理,即可求得 ,根据相似三角形的判定方法,即可得△ODE∽△OBF,△OCE∽△OAF,△OCD∽△OAB,然后由相似三角形的对应边成比例,即可得
,根据相似三角形的判定方法,即可得△ODE∽△OBF,△OCE∽△OAF,△OCD∽△OAB,然后由相似三角形的对应边成比例,即可得 ,
, ,则可求得答案.
,则可求得答案.
解答:∵梯形ABCD中,AB∥CD,
∴ ,△ODE∽△OBF,△OCE∽△OAF,△OCD∽△OAB,
,△ODE∽△OBF,△OCE∽△OAF,△OCD∽△OAB,
∴ ,
, ,
,
∴ .
.
∴在图中与OE:OF的比值相等的线段比有5个.
故选B.
点评:此题考查了平行线分线段成比例定理与相似三角形的判定与性质.此题难度不大,解题的关键是注意数形结合思想的应用,小心别漏解.
分析:由梯形ABCD中,AB∥CD,根据平行线分线段成比例定理,即可求得
 ,根据相似三角形的判定方法,即可得△ODE∽△OBF,△OCE∽△OAF,△OCD∽△OAB,然后由相似三角形的对应边成比例,即可得
,根据相似三角形的判定方法,即可得△ODE∽△OBF,△OCE∽△OAF,△OCD∽△OAB,然后由相似三角形的对应边成比例,即可得 ,
, ,则可求得答案.
,则可求得答案.解答:∵梯形ABCD中,AB∥CD,
∴
 ,△ODE∽△OBF,△OCE∽△OAF,△OCD∽△OAB,
,△ODE∽△OBF,△OCE∽△OAF,△OCD∽△OAB,∴
 ,
, ,
,∴
 .
.∴在图中与OE:OF的比值相等的线段比有5个.
故选B.
点评:此题考查了平行线分线段成比例定理与相似三角形的判定与性质.此题难度不大,解题的关键是注意数形结合思想的应用,小心别漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

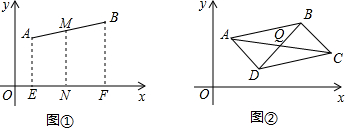 让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系.
让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系.