Question

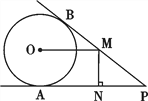
【题目】如图1，平面内，，，.

（1）求证：；

（2）当时，取的中点分别为，连接，如图2，判断的形状，并加以证明.

Answer 1

【答案】（1）证明见解析；（2）△AMN为等腰直角三角形，证明见解析．

【解析】

（1）由可得，根据，，，利用SAS即可判定△ACD≌△ABE即可解决问题；

（2）先根据SAS判定△ABM≌△ACN，再根据全等三角形的性质，得出AM=AM，∠CAN=∠BAM，最后根据∠BAC=90°即可得到∠MAN=90°，进而得到△AMN为等腰直角三角形．

（1）如图1，∵，

∴，

在△DAC和△BAE中，

，

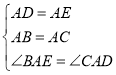∴△DAC≌△BAE（SAS），

∴;

（2）△AMN为等腰直角三角形．

证明：由（1）可得，BE=CD，

∵CD，BE的中点分别为点N、M，

∴BM=CN，

∵△DAC≌△BAE，

∴∠ABM=∠ACN，

在△ABM和△ACN中，

，

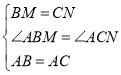∴△ABM≌△ACN（SAS），

∴AM=AN，且∠BAM=∠CAN，

又∵∠CAN+∠NAB=90°，

∴∠MAB+∠BAN=90°，

∴∠MAN=90°，

∴△AMN为等腰直角三角形．