题目内容
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
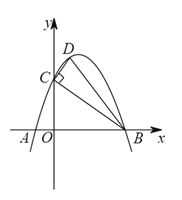
(1)求此抛物线的解析式.
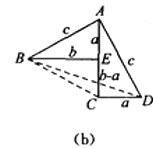
(2)以点![]() 为直角顶点作直角三角形
为直角顶点作直角三角形![]() ,斜边
,斜边![]() 与抛物线交于点
与抛物线交于点![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)将![]() 绕着它的顶点
绕着它的顶点![]() 顺时针在第一象限内旋转,旋转的角度为
顺时针在第一象限内旋转,旋转的角度为![]() ,旋转后的图形为
,旋转后的图形为![]() .当
.当
旋转后的![]() 有一边与
有一边与![]() 重合时,求
重合时,求![]() 不在
不在![]() 上的顶点的坐标.
上的顶点的坐标.
【答案】(![]() )
)![]() (
(![]() )
)![]() ;(
;(![]() )见解析.
)见解析.
【解析】分析:(1)根据抛物线与x轴交于A(-2-n,0),B(4+n,0)两点,根据根与系数的关系求出m的值,从而求出解析式.(2)先求出A、B、C、D的坐标,设出点P 的坐标,由CP=EP即可求解;(3)分两种情况讨论:①![]() 与
与![]() 重合;
重合;![]() 与
与![]() 重合.
重合.
本题解析:
(![]() )
)![]() ,
,
即![]() ,
,
![]() ,
,
![]() .
.
(![]() )
)![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.
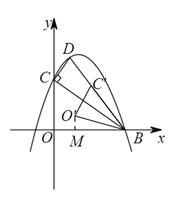
(![]() )①
)①![]() 与
与![]() 重合,
重合,
过![]() 作
作![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
即![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.
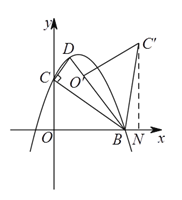
②![]() 与
与![]() 重合时,过
重合时,过![]() 作
作![]() 轴,
轴,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目