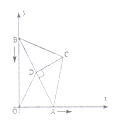
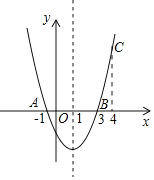题目内容
【题目】如图，在平面直角坐标系
中，已知
，
，
，点
在直线
上，把
沿着直线
翻折，点
落在点
处，联结
，如果直线与直线
所构成的夹角为60°，那么点的坐标是____________
【答案】
或
或
【解析】
先由已知求出
，得出
，
，分
或
两种情况，
当时，又分两种情况：
延长PQ交OB于点N，则
，
，由折叠得出
，求出
，由勾股定理得出
，
，即可得出P点的坐标；
，
，
，即可得出P点的坐标；
当时，Q点与A点重合，
，
，即可得出P点的坐标；
解：
，
，
，
，
，
，
，
，
，
，
，
，
直线PQ与直线AB所构成的夹角为
，
或，
当时，分两种情况：
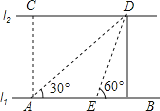
如图1所示：延长PQ交OB于点N，则，
，即，
由折叠得：，
，
，
，
，
，
，
在
中，
，
，
点的坐标为：；
如图2所示：
，，
，
点的坐标为：
；
当时，如图3所示：Q点与A点重合，
由折叠得：，
，
点的坐标为：
；
综上所述：P点的坐标为：或或．
练习册系列答案
阅读快车系列答案
相关题目
