Question

已知：矩形ABCD中，AD=6，AB=8．点P为矩形内一点
（1）过点P作MN∥AD，交AB于点M，交CD于点N．
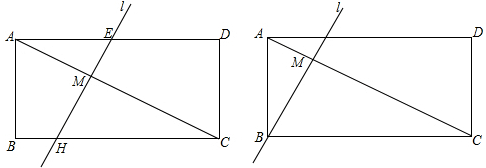
在如图1中，S_△APD+S_△BPC______；
在如图2中，S_△APD+S_△BPC______；
在如图3中，S_△APD+S_△BPC______．

（2）在如图4中，若点P为矩形内任意一点，根据（1）的结论，请你就S_△APD+S_△BPC与矩形ABCD面积的大小提出猜想，并证明你的猜想；
（3）解决问题：
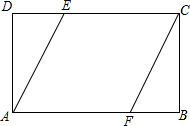
如图5，一个矩形被分成不同的4个三角形，其中绿色的三角形的面积占矩形面积的15%，黄色的三角形的面积是21cm²，求该矩形的面积？

Answer 1

【答案】分析：（1）根据三角形的面积公式求出△APD和△BPC的面积，相加即可得出答案；
（2）S_△APD+S_△BPC与矩形ABCD面积的大小关系是S_△APD+S_△BPC=S_矩形ABCD，过P作MN∥AD，交AB予M，交CD于N，过P作EF⊥AD于E，交BC于F，求出EF=AB=CD，EF⊥BC，根据三角形的面积公式分别求出△APD和△BPC的面积，求出矩形的面积，即可得出答案；
（3）求出黄色占矩形的百分比，再21除以百分比即可得出答案．
解答：（1）解：∵四边形ABCD是矩形，
∴AB∥CD，AD∥BC，AD=BC=6，AB=CD=8，
如图1：S_△APD+S_△BPC=×AD×4+BC×4=×6×4+×6×4=24，
如图2：S_△APD+S_△BPC=×6×2+×6×6=24，
如图3：S_△APD+S_△BPC=×6×5+×6×3=24，
故答案为：24，24，24；

（2）解：S_△APD+S_△BPC与矩形ABCD面积的大小关系是S_△APD+S_△BPC=S_矩形ABCD，
理由是：过P作MN∥AD，交AB予M，交CD于N，过P作EF⊥AD于E，交BC于F，
∵AB∥CD，
∴EF∥AB∥CD，
∵四边形ABCD是矩形，
∴AD∥BC∥MN，
∴EF=AB=CD=8，
∵EF⊥AD，AD∥BC，
∴EF⊥BC，
∴S_△APD+S_△BPC=×AD×PE+×BC×PF，
=AD（PE+PF），
=×AD×EF，
=S_矩形ABCD，
即S_△APD+S_△BPC与矩形ABCD面积的大小关系是S_△APD+S_△BPC=S_矩形ABCD．


（3）解：∵由（2）可知：黄色的三角形占矩形面积的50%-15%=35%，
∴矩形的面积是：21÷35%=60，
答：矩形的面积是60cm²．
点评：本题考查了矩形的性质和三角形的面积公式，主要考查学生的计算能力和观察图象的能力．