题目内容
已知:a、b、c是△ABC三边长,且M=(a+b+c)(a+b-c)(a-b-c),那么
- A.M>0
- B.M=0
- C.M<0
- D.不能确定
C
分析:根据三角形的三边关系,结合有理数乘法法则即可作出选择.
解答:∵a、b、c是△ABC三边长,
∴a+b+c>0,a+b-c>0,a-b-c<0,
∴M=(a+b+c)(a+b-c)(a-b-c)<0.
故选C.
点评:考查了三角形三边关系,解题的关键是根据“三角形两边之和大于第三边”.
分析:根据三角形的三边关系,结合有理数乘法法则即可作出选择.
解答:∵a、b、c是△ABC三边长,
∴a+b+c>0,a+b-c>0,a-b-c<0,
∴M=(a+b+c)(a+b-c)(a-b-c)<0.
故选C.
点评:考查了三角形三边关系,解题的关键是根据“三角形两边之和大于第三边”.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
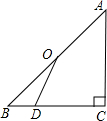 已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.
已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.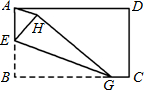 12、如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为
12、如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为