题目内容
等腰三角形两边长为2,5,P为底边上任一点,P到两腰距离之和是________.
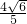
分析:连接AD,根据等腰三角形的性质可表示出S△ABC=S△ABD+S△ACD的值,再根据S△ABC=
 AB•CG,即可得到ED+FD=CG;然后利用三角形的面积求得CG的值.
AB•CG,即可得到ED+FD=CG;然后利用三角形的面积求得CG的值.解答:
 解:如图,过点C作CG⊥AB于点G,过点A作AH⊥BC于点H,连接AD.
解:如图,过点C作CG⊥AB于点G,过点A作AH⊥BC于点H,连接AD.∵2+2<5,
∴等腰△ABC的腰AB=AC=5;
∴AH=
 =2
=2 ;
;有∵AB=AC,
∴S△ABC=S△ABD+S△ACD=
 AB•ED+
AB•ED+ AC•FD=
AC•FD= AB•(ED+FD),
AB•(ED+FD),∴ED+FD=CG;
∵S△ABC=
 AB•CG=
AB•CG= BC•AH,
BC•AH,∴CG=
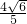 ,即ED+FD=
,即ED+FD=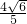 ;
;故答案是:
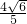 .
.点评:本题综合考查了勾股定理、三角形的面积、等腰三角形的面积.解答此题的关键是求得ED+FD=CG.

练习册系列答案
相关题目