题目内容
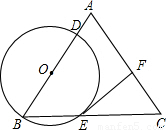
(2005•兰州)如图,已知在△ABC中,AB=AC=6,cosB= ?点O在边AB上,⊙O过点B且分别与边AB、BC交于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.
?点O在边AB上,⊙O过点B且分别与边AB、BC交于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.(1)求证:直线EF是⊙O的切线;
(2)求y关于x的函数关系式(不要求写自变量的取值范围).
【答案】分析:(1)判定直线EF是⊙O的切线,可以证明直线EF垂直于OE即可;
(2)求y关于x的函数关系式可以根据BDE∽△CEF得到关于x,y的关系式,从而得到函数解析式.
解答: (1)证明:连接OE
(1)证明:连接OE
∵AB=AC
∴∠B=∠C
∵OB=OE
∴∠B=∠BEO
∴∠C=∠BEO
∴AC∥OE
∵EF⊥CA
∴EF⊥OE
点E在⊙O上
直线EF是⊙O的切线;
(2)解:过点A作AG⊥BC,垂足为G,
∴BG= AB=2.
AB=2.
∵AB=AC,
∴BC=2BG=4.
∵OB=x,
∴BD=2x.
∵BD是⊙O的直径,
∴∠DEB=90°.
∵cosB= =
= ,
,
∵OB=x,
∴BD=2x,
∴BE= x,
x,
∴CE=BC-BE=4- x.
x.
∵△BDE∽△CEF,
∴ =
= ,
,
∴y=- x+
x+ .
.
点评:本题考查了切线的证明方法,要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.本题是一个函数与相似性相结合的题目,是中考中经常出现的问题.
(2)求y关于x的函数关系式可以根据BDE∽△CEF得到关于x,y的关系式,从而得到函数解析式.
解答:
 (1)证明:连接OE
(1)证明:连接OE∵AB=AC
∴∠B=∠C
∵OB=OE
∴∠B=∠BEO
∴∠C=∠BEO
∴AC∥OE
∵EF⊥CA
∴EF⊥OE
点E在⊙O上
直线EF是⊙O的切线;
(2)解:过点A作AG⊥BC,垂足为G,
∴BG=
 AB=2.
AB=2.∵AB=AC,
∴BC=2BG=4.
∵OB=x,
∴BD=2x.
∵BD是⊙O的直径,
∴∠DEB=90°.
∵cosB=
 =
= ,
,∵OB=x,
∴BD=2x,
∴BE=
 x,
x,∴CE=BC-BE=4-
 x.
x.∵△BDE∽△CEF,
∴
 =
= ,
,∴y=-
 x+
x+ .
.点评:本题考查了切线的证明方法,要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.本题是一个函数与相似性相结合的题目,是中考中经常出现的问题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 ?点O在边AB上,⊙O过点B且分别与边AB、BC交于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.
?点O在边AB上,⊙O过点B且分别与边AB、BC交于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.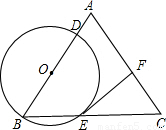
 ?点O在边AB上,⊙O过点B且分别与边AB、BC交于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.
?点O在边AB上,⊙O过点B且分别与边AB、BC交于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.
 ?点O在边AB上,⊙O过点B且分别与边AB、BC交于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.
?点O在边AB上,⊙O过点B且分别与边AB、BC交于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.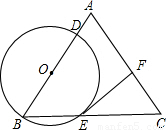
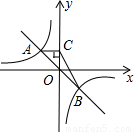
 的图象交于A、B两点,过点A作AC垂直于y轴,垂足为点C,则△BOC的面积为 .
的图象交于A、B两点,过点A作AC垂直于y轴,垂足为点C,则△BOC的面积为 .