题目内容
如图,在▱ABCD中,点E、F分别在边BC和AD上,且BE=DF.
(1)求证:△ABE≌△CDF;
(2)求证:AE=CF.

证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D,
在△ABE和△CDF中,

∴△ABE≌△CDF(SAS),
∴AE=CF.

练习册系列答案
相关题目
下列运算正确的是( )
|
| A. | (m+n)2=m2+n2 | B. | (x3)2=x5 | C. | 5x﹣2x=3 | D. | (a+b)(a﹣b)=a2﹣b2 |
已知等腰△ABC的两边长分别为2和3,则等腰△ABC的周长为( )
|
| A. | 7 | B. | 8 | C. | 6或8 | D. | 7或8 |
湘西盛产椪柑,春节期间,一外地运销客户安排15辆汽车装运A、B、C三种不同品质的椪柑120吨到外地销售,按计划15辆汽车都要装满且每辆汽车只能装同一种品质的椪柑,每种椪柑所用车辆部不少于3辆.
(1)设装运A种椪柑的车辆数为x辆,装运B种椪柑车辆数为y辆,根据下表提供的信息,求出y与x之间的函数关系式;
| 椪柑品种 | A | B | C |
| 每辆汽车运载量 | 10 | 8 | 6 |
| 每吨椪柑获利(元) | 800 | 1200 | 1000 |
(2)在(1)条件下,求出该函数自变量x的取值范围,车辆的安排方案共有几种?请写出每种安排方案;
(3)为了减少椪柑积压,湘西州制定出台了促进椪柑销售的优惠政策,在外地运销客户原有获利不变的情况下,政府对外地运销客户,按每吨50元的标准实行运费补贴.若要使该外地运销客户所获利润W(元)最大,应采用哪种车辆安排方案?并求出利润W(元)的最大值?
在2014年5月崇左市教育局举行的“经典诗朗诵”演讲比赛中,有11名学生参加决赛,他们决赛的成绩各不相同,其中的一名学生想知道自己能否进入前6名,不仅要了解自己的成绩,还要了解这11名学生成绩的( )
|
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 方差 |
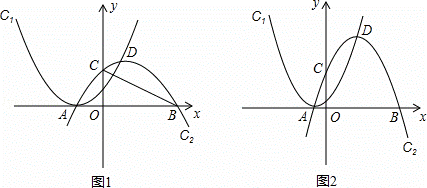
 P的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;
P的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;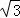 ﹣m(0<m<
﹣m(0<m<