题目内容
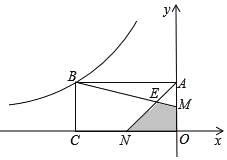
【题目】如图,矩形OABC的两边OA、OC在坐标轴上,且OC=2OA,M、N分别为OA、OC的中点,BM与AN交于点E,若四边形EMON的面积为2,则经过点B的双曲线的解析式为( )
A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=﹣
D. y=﹣![]()
【答案】A
【解析】过M作MG∥ON,交AN于G,过E作EF⊥AB于F,如图所示:
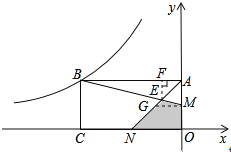
设EF=h,OM=a,
那么由题意可知:AM=OM=a,ON=NC=2a,AB=OC=4a,BC=AO=2a
△AON中,MG∥ON,AM=OM,
∴MG=![]() ON=a,
ON=a,
∵MG∥AB
∴![]() =
=![]() =
=![]() ,
,
∴BE=4EM,
∵EF⊥AB,
∴EF∥AM,
∴![]() =
=![]() =
=![]() .
.
∴FE=![]() AM,即h=
AM,即h=![]() a,
a,
∵S△ABM=4a×a÷2=2a2,
S△AON=2a×2a÷2=2a2,
∴S△ABM=S△AON,
∴S△AEB=S四边形EMON=2,
S△AEB=AB×EF÷2=4a×h÷2=2,
ah=1,又有h=![]() a,a=
a,a=![]() (长度为正数)
(长度为正数)
∴OA=![]() ,OC=2
,OC=2![]() ,因此B的坐标为(-2
,因此B的坐标为(-2![]() ,
,![]() ),
),
那么经过B的双曲线的解析式就是y=-![]() ;
;
故选A。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目