Question

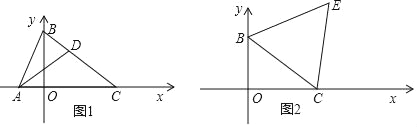
【题目】在平面直角坐标系xOy中，点B（0，3），点C（4，0）

（1）求线段BC的长．

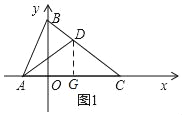
（2）如图1，点A（﹣1，0），D是线段BC上的一点，若△BAD∽△BCA时，求点D的坐标．

（3）如图2，以BC为边在第一象限内作等边△BCE，求点E的坐标．

Answer 1

【答案】（1）BC=5；（2）D（1.6，1.8）；（3）点E的坐标为（2+，）．

【解析】

（1）已知点B（0，3），点C（4，0），即可得到BO=3，CO=4，根据勾股定理求得BC=5；

（2）已知点A（﹣1，0），可得AO=1，得出AB2=AO2+BO2=10，再根据△BAD∽△BCA，即可得出AB2=BD×BC，求得BD=2，CD=3，过D作DG⊥AC于G，即可得DG∥BO，所以，由此可求得DG=1.8，CG=2.4，OG=1.6，即可得到D（1.6，1.8）；（3）过E作EF⊥OC于F，EH⊥BO于H，设E（x，y），则EH=OF=x，EF=HO=y，得出HB=y﹣3，CF=x﹣4，依据勾股定理可得HE2+HB2=BE2=CE2=CF2+EF2，即x2+（y﹣3）2=25=（x﹣4）2+y2，进而得出点E的坐标．

解：（1）如图1，∵点B（0，3），点C（4，0），

∴BO=3，CO=4，

∴BC==5；

（2）∵点A（﹣1，0），

∴AO=1，

∴AB2=AO2+BO2=10，

∵△BAD∽△BCA，

∴=，即AB2=BD×BC，

∴10=BD×5，

解得BD=2，

∴CD=3，

如图1，过D作DG⊥AC于G，则DG∥BO，

∴，即==，

解得DG=1.8，CG=2.4，

∴OG=1.6，

∴D（1.6，1.8）；

（3）如图2，过E作EF⊥OC于F，EH⊥BO于H，

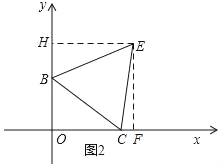
设E（x，y），则EH=OF=x，EF=HO=y，

∴HB=y﹣3，CF=x﹣4，

∵HE2+HB2=BE2=CE2=CF2+EF2，

即x2+（y﹣3）2=25=（x﹣4）2+y2，

解得x1=2+，x2=2﹣（舍去），

∴y=+2，

∴点E的坐标为（2+，）．