��Ŀ����
����Ŀ��̽������㣺
�ڡ�ABC�У�BE��AC�ڵ�E��CD��AB�ڵ�D������DE��
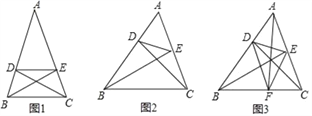
��1����ͼ1������A=45�㣬AB=AC��BC=4����DE�ij���
��2����ͼ2������A=60�㣬AB��AC����ȣ�BC=4����DE�ij���
������֤����
��3�����ݣ�1����2��������Ľ��������DE��BC�Լ���A֮���������ϵ����֤����
��չ��Ӧ�ã�
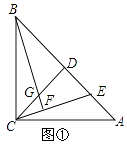
��4����ͼ3���ڡ�ABC�У�AB=BC=5��AC=2![]() ��BE��AC�ڵ�E��CD��AB�ڵ�D��AF��BC�ڵ�F�����DEF���ܳ���
��BE��AC�ڵ�E��CD��AB�ڵ�D��AF��BC�ڵ�F�����DEF���ܳ���
���𰸡�(1) DE=2![]() ��(2) DE =2��(3) DE=BCcosA,֤��������;(4) ��DEF���ܳ�=
��(2) DE =2��(3) DE=BCcosA,֤��������;(4) ��DEF���ܳ�=![]() .
.
�������������������1�����ݵ���ֱ�������ε����ʵõ�AE=BE=![]() AB���������������ε��ж������õ���ADE�ס�ABC���������������ε����ʼ��㣻
AB���������������ε��ж������õ���ADE�ס�ABC���������������ε����ʼ��㣻
��2������ֱ�������ε����ʵõ�AE=![]() AB��AD=
AB��AD=![]() AC���������������ε��ж������õ���ADE�ס�ACB���������������ε����ʼ��㣻
AC���������������ε��ж������õ���ADE�ס�ACB���������������ε����ʼ��㣻
��3���������ҵĸ�����������ε��ж������ʽ��
��4�����ݣ�3���Ľ��ۡ������ε������ʽ�����ɶ������㼴�ɣ�
���������
��1����BE��AC����A=45�㣬
��AE=BE=![]() AB��
AB��
ͬ����AD=CD=![]() AC��
AC��
��AB=AC��
��AE=AD��
��![]() =
=![]() ������A=��A��
������A=��A��
���ADE�ס�ABC��
��![]() =
=![]() =
=![]() ��
��
��DE=2![]() ��
��
��2����BE��AC����A=60�㣬
��AE=![]() AB��
AB��
ͬ����AD=![]() AC��
AC��
��![]() =
=![]() ������A=��A��
������A=��A��
���ADE�ס�ACB��
��![]() =
=![]() ��
��
��DE=![]() BC=2��
BC=2��
��3�����룺DE=BCcosA��
֤������BE��AC��
��cosA=![]() ��
��
��AE=ABcosA��
ͬ����AD=ACcosA��
����ADE�ס�ACB��
��![]() =cosA��
=cosA��
��DE=BCcosA��
��4����AB=BC=5��AC=2![]() ��BE��AC��
��BE��AC��
��AE=EC=![]() ��
��
�ɹ��ɶ����ã�BE=![]() =2
=2![]() ��
��
��BC��AF=AC��BE��
��AF=4��
�ɹ��ɶ����ã�BF=3��
��cos��ABC=![]() =
=![]() ��cos��ACB=cos��BAC=
��cos��ACB=cos��BAC=![]() ��
��
��EF=DE=ABcos��ACB=![]() ��DF=ACcos��ABC=
��DF=ACcos��ABC=![]() ��
��
���DEF���ܳ�=DE+EF+DF=![]() ��
��