题目内容
如图，△ABC是一个中心对称图形的一部分，O点是对称中心，点A和点B是一对对应点，∠C=90°，那么将这个图形补成一个完整的图形是
- A.矩形
- B.菱形
- C.正方形
- D.梯形
A
分析：作出图形，根据中心对称的性质可得AC′=BC，BC′=AC，然后根据两组对比分别相等的四边形是平行四边形，再根据一个角是直角的平行四边形是矩形解答．
解答：
解：如图，∵O点是对称中心，△A′B′C′是△ABC关于点O的对称图形，
∴AC′=BC，BC′=AC，
∴四边形ABC′A是平行四边形，
∵∠C=90°，
∴平行四边形ABC′A是矩形．
故选A．
点评：本题考查了中心对称，平行四边形的判定，矩形的判定，根据中心对称的性质得到相等的对应边是解题的关键，作出图形更形象直观．
分析：作出图形，根据中心对称的性质可得AC′=BC，BC′=AC，然后根据两组对比分别相等的四边形是平行四边形，再根据一个角是直角的平行四边形是矩形解答．
解答：
解：如图，∵O点是对称中心，△A′B′C′是△ABC关于点O的对称图形，∴AC′=BC，BC′=AC，
∴四边形ABC′A是平行四边形，
∵∠C=90°，
∴平行四边形ABC′A是矩形．
故选A．
点评：本题考查了中心对称，平行四边形的判定，矩形的判定，根据中心对称的性质得到相等的对应边是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
2、如图，△ABC是一个等边三角形，它绕着点P旋转，可以与等边△ABD重合，则这样的点P有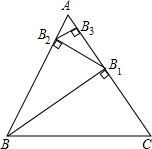
如图，△ABC是一个边长为1的等边三角形，BB1是△ABC的高，B1B2是△ABB1的高，B2B3是△AB1B2的高，B3B4是△AB2B3的高，…Bn-1Bn是△ABn-2Bn-1的高
如图，△ABC是一个圆锥的左视图，其中AB=AC=5，BC=8，则这个圆锥的侧面积是
如图，△ABC是一个等腰三角形，直角边的长度是1米，现在以点C为圆心，把三角形ABC顺时针旋转90度，那么，AB边在旋转时所扫过的面积是（ ）平方米．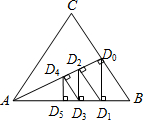
（2013•怀柔区一模）如图，△ABC是一个边长为2的等边三角形，AD0⊥BC，垂足为点D0．过点D0作D0D1⊥AB，垂足为点D1；再过点D1作D1D2⊥AD0，垂足为点D2；又过点D2作D2D3⊥AB，垂足为点D3；…；这样一直作下去，得到一组线段：D0D1，D1D2，D2D3，…，则线段D1D2的长为