��Ŀ����
�������壺��һ��ֱ����һ��������ֻ��һ�������㣬������ֱ�������������ߵĶԳ��ƽ�У��ͳ�ֱ�������������У�����ֱ���������ߵ����ߣ����������⣺
��ֱ��y=0��������y=
x2�����ߣ�
��ֱ��x=-2��������y=
x2�����ڵ㣨-2��1����
����ֱ��y=x+b��������y=
x2���У��������ڵ㣨2��1����
����ֱ��y=kx-2��������y=
x2���У���ʵ��k=
��
������ȷ������ǣ�������
��ֱ��y=0��������y=
| 1 |
| 4 |
��ֱ��x=-2��������y=
| 1 |
| 4 |
����ֱ��y=x+b��������y=
| 1 |
| 4 |
����ֱ��y=kx-2��������y=
| 1 |
| 4 |
| 2 |
������ȷ������ǣ�������
| A���٢ڢ� | B���٢� | C���ڢ� | D���٢ۢ� |
�١�ֱ��y=0��x�ᣬ������y=
x2�Ķ�����x���ϣ���ֱ��y=0��������y=
x2�����ߣ��ʱ�С����ȷ��
�ڡ�������y=
x2�Ķ�����x���ϣ��������ϣ�ֱ��x=-2��y��ƽ�У���ֱ��x=-2��������y=
x2�ཻ���ʱ�С�����
�ۡ�ֱ��y=x+b��������y=
x2������
x2-x-b=0�����=��-1��2-4��
b=1+b=0�����b=-1����b=-1����
x2-x-b=0��x=2����x=2���������߽���ʽ��֪y=1����ֱ��y=x+b��������y=
x2���У��������ڵ㣨2��1�����ʱ�С����ȷ��
�ܡ�ֱ��y=kx-2��������y=
x2������
x2=kx-2����
x2-kx+2=0����=k2-2=0�����k=��
���ʱ�С�����
��ѡB��
| 1 |
| 4 |
| 1 |
| 4 |
�ڡ�������y=
| 1 |
| 4 |
| 1 |
| 4 |
�ۡ�ֱ��y=x+b��������y=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
�ܡ�ֱ��y=kx-2��������y=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
��ѡB��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ

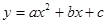 ��ͼ���A��2��0����B��0��-1����C��4��5�����㡣
��ͼ���A��2��0����B��0��-1����C��4��5�����㡣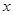 �����һ������ΪD�����D�����ꣻ
�����һ������ΪD�����D�����ꣻ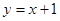 ����д����
�������