题目内容
已知
，求
的值。
、
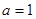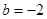原式的值为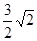
解析试题分析：由可得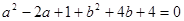
，根据完全平方公式分解可得
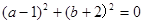，根据非负数的性质即可求得
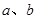的值，再代入即可求得结果.
∴
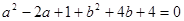
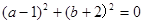
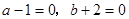
解得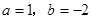
则
.
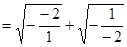
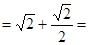
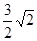考点：非负数的性质，二次根式的化简
点评：解题的关键是熟记非负数的性质：若两个非负数的和为0，这两个数均为0.
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
已知，求的值。
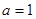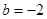、 原式的值为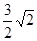
解析试题分析：由可得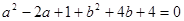，根据完全平方公式分解可得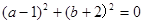，根据非负数的性质即可求得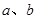的值，再代入即可求得结果.
∴
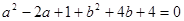
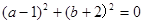
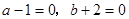
解得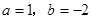
则.
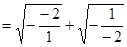
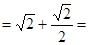
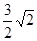考点：非负数的性质，二次根式的化简
点评：解题的关键是熟记非负数的性质：若两个非负数的和为0，这两个数均为0.
名校课堂系列答案
，求
的值．
，求
的值.
，求
的值．
，求
的值
的值
，求
的值