题目内容
【题目】已知:关于x的方程kx2﹣(3k﹣1)x+2(k﹣1)=0
(1)求证:无论k为任何实数,方程总有实数根;
(2)若此方程有两个实数根x1,x2,且|x1﹣x2|=2,求k的值.
【答案】(1)证明详见解析;(2) 1或![]() .
.
【解析】试题分析:(1)确定判别式的范围即可得出结论;
(2)根据根与系数的关系表示出x1+x2,x1x2,继而根据题意得出方程,解出即可.
(1)证明:①当k=0时,方程是一元一次方程,有实数根;
②当k≠0时,方程是一元二次方程,
∵△=(3k﹣1)2﹣4k×2(k﹣1)=(k+1)2≥0,
∴无论k为任何实数,方程总有实数根.
(2)解:∵此方程有两个实数根x1,x2,
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∵|x1﹣x2|=2,
∴(x1﹣x2)2=4,
∴(x1+x2)2﹣4x1x2=4,即![]() ﹣4×
﹣4×![]() =4,
=4,
解得:![]() =±2,
=±2,
即k=1或k=﹣,
经检验k=1或k=﹣是方程的解,
则k=1或k=﹣.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
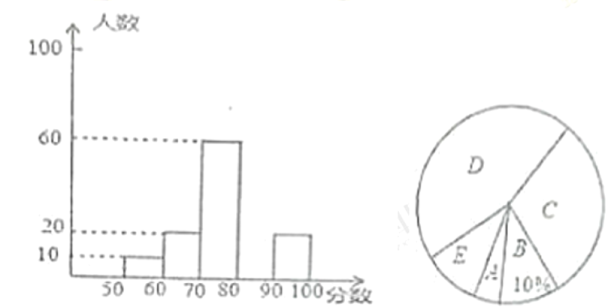
【题目】七年级数学研究学习小组在某↑字路口随机调查部分市民对“社会主义核心价值观”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:
得分 | |
|
|
|
|
|
|
|
|
|
|
(1)本次调查的总人数为 人, 在扇形统计图中“心所在扇形的圆心角的度数为 :
(2)补全频数分布图:
(3)若在这周里,该路口共有![]() 人通过,请估计得分超过
人通过,请估计得分超过![]() 的约有多少人?
的约有多少人?