题目内容
 (2013•河南)我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的宽度AC(结果精确到0.1米.参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,
(2013•河南)我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的宽度AC(结果精确到0.1米.参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50,| 3 |
分析:在Rt△BAE中,根据BE=162米,∠BAE=68°,解直角三角形求出AE的长度,然后在Rt△DCE中解直角三角形求出CE的长度,然后根据AC=CE-AE求出AC的长度即可.
解答:解:在Rt△BAE中,
∵BE=162米,∠BAE=68°,
∴AE=
=
=64.8(米),
在Rt△DCE中,
∵DE=176.6米,∠DCE=60°,
∴CE=
=
=
≈102.1(米),
则AC=CE-AE=102.1-64.8=37.3(米).
答:工程完工后背水坡坡底端水平方向增加的宽度AC约为37.3米.
∵BE=162米,∠BAE=68°,
∴AE=
| BE |
| tan68° |
| 162 |
| 2.50 |
在Rt△DCE中,
∵DE=176.6米,∠DCE=60°,
∴CE=
| DE |
| tan60° |
| 176.6 | ||
|
| 176.6 |
| 1.73 |
则AC=CE-AE=102.1-64.8=37.3(米).
答:工程完工后背水坡坡底端水平方向增加的宽度AC约为37.3米.
点评:本题考查了解直角三角形的应用,难度适中,解答本题的关键是构造直角三角形并解直角三角形.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 (2013•河南)将一副直角三角板ABC和EDF如图放置(其中∠A=60°,∠F=45°).使点E落在AC边上,且ED∥BC,则∠CEF的度数为
(2013•河南)将一副直角三角板ABC和EDF如图放置(其中∠A=60°,∠F=45°).使点E落在AC边上,且ED∥BC,则∠CEF的度数为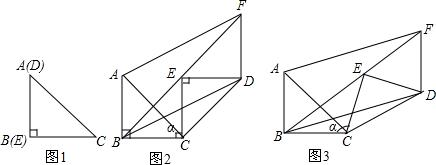
 (2013•河南模拟)若b>0,二次函数y=ax2+bx+a2-1的图象如图,则a等于
(2013•河南模拟)若b>0,二次函数y=ax2+bx+a2-1的图象如图,则a等于