题目内容
如图(1),四边形ABCD是⊙O的内接四边形,点C是 的中点,过点C的切线与AD的延长线交于点E.
的中点,过点C的切线与AD的延长线交于点E.(1)求证:AB•DE=CD•BC;
(2)如果四边形ABCD仍是⊙O的内接四边形,点C在劣弧
 上运动,点E在AD的延长线上运动,切线CE变为割线EFC,请问要使(1)的结论成立还需要具备什么条件?请你在图(2)上画出示意图,标明有关字母,不要求进行证明.
上运动,点E在AD的延长线上运动,切线CE变为割线EFC,请问要使(1)的结论成立还需要具备什么条件?请你在图(2)上画出示意图,标明有关字母,不要求进行证明.
【答案】分析:(1)可通过构建相似三角形来求证,连接AC证三角形ABC和CDE相似,CE是圆的切线,根据弦切角定理可得出∠DCE=∠CAD,根据C是弧BD的中点,得出∠BAC=∠DAC,那么∠DCE=∠BAC,根据ABCD内接于圆O,那么外角∠CDE=∠B,那么就构成了两三角形相似的条件,得出相似后,即可得出所要求证的比例关系;
(2)要使(1)的条件成立,就必须保证△ABC和△CDE相似,因此就要保证∠DCF=∠BAC,那么需要满足的条件就应该是 (也可以写成角相等,线段相等或平行等样式).
(也可以写成角相等,线段相等或平行等样式).
解答: (1)证明:连接AC.
(1)证明:连接AC.
∵C是 的中点,
的中点,
∴ ,∠BAC=∠DAC
,∠BAC=∠DAC
∵CE切⊙O于点C,点C在⊙O上
∴∠DCE=∠DAC=∠BAC,
∵四边形ABCD是⊙O的内接四边形,
∴∠EDC=∠B,
∴△EDC∽△CBA,
∴ ,
,
∴AB•DE=CD•BC;
(2)解:如图,条件为: (或DF=BC或∠DAF=∠BAC
(或DF=BC或∠DAF=∠BAC
或∠DCF=∠BAC或FC∥BD等)
如图,(图中虚线为可能画的线).
点评:本题主要考查了圆的内接四边形,相似三角形的判定和性质等知识点,通过构建相似三角形来来求解是解题的关键.
(2)要使(1)的条件成立,就必须保证△ABC和△CDE相似,因此就要保证∠DCF=∠BAC,那么需要满足的条件就应该是
 (也可以写成角相等,线段相等或平行等样式).
(也可以写成角相等,线段相等或平行等样式).解答:
 (1)证明:连接AC.
(1)证明:连接AC.∵C是
 的中点,
的中点,∴
 ,∠BAC=∠DAC
,∠BAC=∠DAC∵CE切⊙O于点C,点C在⊙O上
∴∠DCE=∠DAC=∠BAC,
∵四边形ABCD是⊙O的内接四边形,
∴∠EDC=∠B,
∴△EDC∽△CBA,
∴
 ,
,∴AB•DE=CD•BC;
(2)解:如图,条件为:
 (或DF=BC或∠DAF=∠BAC
(或DF=BC或∠DAF=∠BAC或∠DCF=∠BAC或FC∥BD等)
如图,(图中虚线为可能画的线).
点评:本题主要考查了圆的内接四边形,相似三角形的判定和性质等知识点,通过构建相似三角形来来求解是解题的关键.

练习册系列答案
相关题目
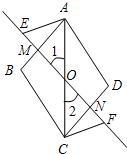 56、如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.
56、如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF. 18、如图,已知平行四边形ABCD.
18、如图,已知平行四边形ABCD.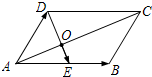 如图,已知平行四边形ABCD,E是边AB的中点,连接AC、DE交于点O.记向量
如图,已知平行四边形ABCD,E是边AB的中点,连接AC、DE交于点O.记向量
 画出如图所示的平行四边形ABCD绕点D顺时针旋转90°后的图形,再经几次90°旋转可以与原来图形重合.
画出如图所示的平行四边形ABCD绕点D顺时针旋转90°后的图形,再经几次90°旋转可以与原来图形重合.