题目内容
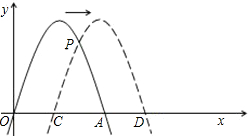
已知经过原点的抛物线y=-2x2+4x(如图所示)与x的另一交点为A现将它向右平移m(m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P(1)求点P的坐标(可用含m式子表示);
(2)设△PCD的面积为s,求s关于m关系式;
(3)过点P作x轴的平行线交原抛物线于点E,交平移后的抛物线于点F.请问是否存在m,使以点E、O、A、F为顶点的四边形为平行四边形?若存在,求出m的值;若不存在,请说明理由.

【答案】分析:(1)首先将抛物线表示出顶点式的形式,再进行平移,左加右减,即可得出答案;
(2)求出抛物线与x轴的交点坐标,根据当0<m<2,当m=2,即点P在x轴时,当m>2即点P在第四象限时,分别得出即可;
(3)根据E、O、A、F为顶点的四边形是平行四边形,则EF=OA=2由轴对称可知PE=PF,表示出E点的坐标,再把点E代入抛物线解析式得出即可.
解答: 解:(1)原抛物线:y=-2x2+4x=-2(x-1)2+2,
解:(1)原抛物线:y=-2x2+4x=-2(x-1)2+2,
则平移后的抛物线为:y=-2(x-1-m)2+2,
由题得 ,
,
解得 ,
,
∴点P的坐标为( ,
, );
);
(2)抛物线:y=-2x2+4x=-2x(x-2)
∴抛物线与x轴的交点为O(0,0)A(2,0),
∴AO=2,
∵C、D两点是抛物线y=-2x2+4x向右平移m(m>0)个,
单位所得抛物线与x轴的交点∴CD=OA=2,
①当0<m<2,即点P在第一象限时,如图1,作PH⊥x轴于H.
∵P的坐标为( ,
, ),
),
∴PH= ,
,
∴S= CD•2•(-
CD•2•(- m2+2)=-
m2+2)=- m2+2,
m2+2,
②当m=2,即点P在x轴时,△PCD不存在,
③当m>2即点P在第四象限时,如图2,作PH⊥x轴于H.
∵P的坐标为( ,
, ),
),
∴PH= ,
,
∴S= CD•HP=
CD•HP= ×2×
×2× =
= m2-2;
m2-2;

(3)如图3,若以E、O、A、F为顶点的四边形是平行四边形,则EF=OA=2
由轴对称可知PE=PF,
∴PE= ,
,
∵P( ,
, ),
),
∴点E的坐标为( ,
, ),
),
把点E代入抛物线解析式得: ,
,
解得:m=1.
点评:此题主要考查了二次函数解析式的顶点坐标求法以及平行四边形的判定,题目综合性较强,从题目问题开始逐步分析,是解决问题的关键.
(2)求出抛物线与x轴的交点坐标,根据当0<m<2,当m=2,即点P在x轴时,当m>2即点P在第四象限时,分别得出即可;
(3)根据E、O、A、F为顶点的四边形是平行四边形,则EF=OA=2由轴对称可知PE=PF,表示出E点的坐标,再把点E代入抛物线解析式得出即可.
解答:
 解:(1)原抛物线:y=-2x2+4x=-2(x-1)2+2,
解:(1)原抛物线:y=-2x2+4x=-2(x-1)2+2,则平移后的抛物线为:y=-2(x-1-m)2+2,
由题得
 ,
,解得
 ,
,∴点P的坐标为(
 ,
, );
);(2)抛物线:y=-2x2+4x=-2x(x-2)
∴抛物线与x轴的交点为O(0,0)A(2,0),

∴AO=2,
∵C、D两点是抛物线y=-2x2+4x向右平移m(m>0)个,
单位所得抛物线与x轴的交点∴CD=OA=2,
①当0<m<2,即点P在第一象限时,如图1,作PH⊥x轴于H.
∵P的坐标为(
 ,
, ),
),∴PH=
 ,
,∴S=
 CD•2•(-
CD•2•(- m2+2)=-
m2+2)=- m2+2,
m2+2,②当m=2,即点P在x轴时,△PCD不存在,
③当m>2即点P在第四象限时,如图2,作PH⊥x轴于H.
∵P的坐标为(
 ,
, ),
),∴PH=
 ,
,∴S=
 CD•HP=
CD•HP= ×2×
×2× =
= m2-2;
m2-2;
(3)如图3,若以E、O、A、F为顶点的四边形是平行四边形,则EF=OA=2
由轴对称可知PE=PF,
∴PE=
 ,
,∵P(
 ,
, ),
),∴点E的坐标为(
 ,
, ),
),把点E代入抛物线解析式得:
 ,
,解得:m=1.
点评:此题主要考查了二次函数解析式的顶点坐标求法以及平行四边形的判定,题目综合性较强,从题目问题开始逐步分析,是解决问题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 们的长度(可用含m的式子表示);若不存在,请说明理由;
们的长度(可用含m的式子表示);若不存在,请说明理由;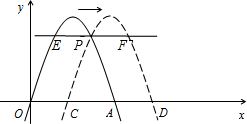 右平移m(m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P
右平移m(m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P

