Question

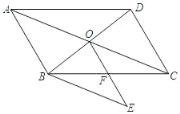
【题目】如图，在□ABCD中，AC与BD相交于点O，过点B作BE∥AC，联结OE交BC于点F，点F为BC的中点．

（1）求证：四边形AOEB是平行四边形；

（2）如果∠OBC＝∠E，求证：BOOC＝ABFC．

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）根据BE∥AC，△COF∽△BEF，又因为F为BC的中点可得CF=BF，所以BE=OC=OA，结合BE∥AC，即可证得AOEB是平行四边形.

（2）根据题意可证得△COB∽△CBA，即，在依据AC＝2OC，BC＝2FC，可得，即可证得BOOC＝ABFC

（1）∵BE∥AC，

∴△COF∽△BEF

∴

∵点F为BC的中点，

∴CF＝BF，

∴OC＝BE

∵四边形ABCD是平行四边形，

∴AO＝CO

∴AO＝BE

∵BE∥AC，

∴四边形AOEB是平行四边形

（2）∵四边形AOEB是平行四边形，

∴∠BAO＝∠E

∵∠OBC＝∠E，

∴∠BAO＝∠OBC

∵∠ACB＝∠BCO，

∴△COB∽△CBA

∴

∵四边形ABCD是平行四边形，

∴AC＝2OC

∵点F为BC的中点，

∴BC＝2FC

∴

即BOOC＝ABFC.