题目内容
如图,在平面直角坐标系xOy中,顶点为M的抛物线 经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
(1)求这条抛物线的表达式;
(2)连接OM,求∠AOM的大小;
(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.
解:(1)如图,过点A作AD⊥y轴于点D,
∵AO=OB=2,∴B(2,0)。
∵∠AOB=1200,∴∠AOD=300,∴AD=1,OD=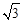 。
。
∴A(-1,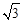 )。
)。
将A(-1,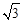 ),B(2,0)代入
),B(2,0)代入 ,得:
,得: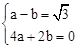 ,解得
,解得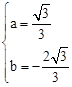 。
。
∴这条抛物线的表达式为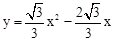 。
。
(2)过点M作ME⊥x轴于点E,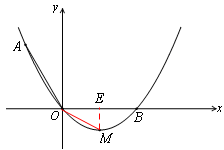
∵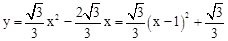 。
。
∴M(1,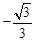 ),即OE=1,EM=
),即OE=1,EM=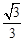 。
。
∴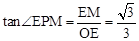 。∴
。∴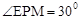 。
。
∴ 。
。
(3)过点A作AH⊥x轴于点H ,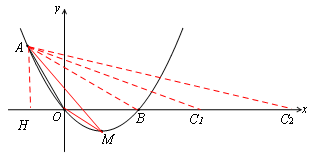
∵AH=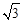 ,HB=HO+OB=3,
,HB=HO+OB=3,
∴ 。
。
∴ ,∴
,∴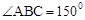 。
。
∴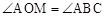 。
。
∴要△ABC与△AOM相似,则必须:
①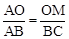 ,或②
,或②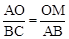 。
。
设点C的坐标为(c,0),则根据坐标和勾股定理,有
AO=2,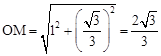 ,
,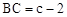 ,
, 。
。
①由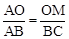 得,
得, ,解得
,解得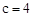 。∴C1(4,0)。
。∴C1(4,0)。
②由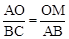 得,
得,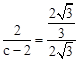 ,解得
,解得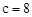 。∴C2(8,0)。
。∴C2(8,0)。
综上所述,如果点C在x轴上,且△ABC与△AOM相似,则点C的坐标为(4,0)或(8,0)。
解析试题分析:(1)应用三角函数求出点A的坐标,将A,B的坐标代入 ,即可求得a、b,从而求得抛物线的表达式。
,即可求得a、b,从而求得抛物线的表达式。
(2)应用二次函数的性质,求出点M的坐标,从而求得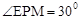 ,进而求得∠AOM的大小。
,进而求得∠AOM的大小。
(3)由于可得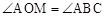 ,根据相似三角形的判定,分
,根据相似三角形的判定,分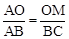 ,
,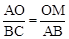 两种情况讨论。
两种情况讨论。

练习册系列答案
相关题目
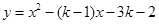 与
与 轴交于两点A
轴交于两点A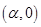 ,B
,B ,且
,且 ,求k的值.
,求k的值. (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.

 (元)与销售单价
(元)与销售单价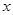 (元)之间的函数关系式;
(元)之间的函数关系式; 经过A、C两点,与x轴的另一个交点是点D,连接BD.
经过A、C两点,与x轴的另一个交点是点D,连接BD.
 的图象经过点A,B,与x轴分别交于点E,F,且点E的坐标为(
的图象经过点A,B,与x轴分别交于点E,F,且点E的坐标为(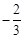 ,0),以OC为直径作半圆,圆心为D.
,0),以OC为直径作半圆,圆心为D.

 ?若存在,求出点Q的坐标;若不存在,请说明理由。
?若存在,求出点Q的坐标;若不存在,请说明理由。