题目内容
在锐角△ABC中,直线l为BC的中垂线,直线m为∠ABC的角平分线,且l与m相交于点P.若∠A=60°,∠ACP=24°,求∠ABP的度数.

32°.
【解析】
试题分析:根据角平分线的性质可得∠ABP=∠CBP,根据中垂线的性质可得∠CBP=∠BCP,然后根据△ABC的内角和定理进行求解.
试题解析: 直线m为∠ABC的角平分线,∴∠ABP=∠CBP
直线m为∠ABC的角平分线,∴∠ABP=∠CBP
∵直线l为BC的中垂线,∴PB=PC ∴∠CBP=∠BCP
∴∠ABP=∠CBP=∠BCP
在锐角△ABC中,3∠ABP+∠A+∠ACP=180°
又∵∠A=60°,∠ACP=24° ∴∠ABP=32°.
考点:三角形内角和定理、等腰三角形的性质.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 少3元.问甲、乙两件商品的价格各多少元?
少3元.问甲、乙两件商品的价格各多少元?  ”标志,并在正方体的每个表面都画了黑色粗线,如右图所示.在下列图形中,是这个正方体包装盒的表面展开图的是
”标志,并在正方体的每个表面都画了黑色粗线,如右图所示.在下列图形中,是这个正方体包装盒的表面展开图的是


 -
-

 (2)、
(2)、
 的值为零,则x的值为 .
的值为零,则x的值为 . 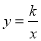 的图象与一次函数
的图象与一次函数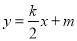 的图象交点为(2,2).
的图象交点为(2,2).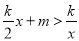 的解集.
的解集.