题目内容
22、如图：以△ABC的边AB、AC为边分别向外作正方形ADEB、ACGF，连接DC、BF相交于M，DC、AB相交于N．（1）从旋转的角度看，△ADC是绕点
A
逆时针旋转90
度，可以得到△ABF．（2）CD与BF有何关系？请说明理由．
分析：（1）找准一边看清旋转角度，两个三角形的公共点为旋转中心．
（2）DC=BF且DC⊥BF，可以利用△ADC≌△ABF（SAS）来证明相等，∠ABM+∠BNM=∠NMB=90°来证明垂直．
（2）DC=BF且DC⊥BF，可以利用△ADC≌△ABF（SAS）来证明相等，∠ABM+∠BNM=∠NMB=90°来证明垂直．
解答：解：（1）A，90（2分）
（2）DC=BF且DC⊥BF（4分）
理由：∵∠DAB=∠CAF=90°
∴∠DAC=∠BAF（等量加等量和相等）
又∵AD=ABAC=AF
∴△ADC≌△ABF（SAS）（6分）
∴∠AND=∠ABMDC=BF
又∵∠AND+∠DNA=90°
∴∠ABM+∠BNM=90°
∴∠NMB=90°
即DC⊥BF．（8分）
（2）DC=BF且DC⊥BF（4分）
理由：∵∠DAB=∠CAF=90°
∴∠DAC=∠BAF（等量加等量和相等）
又∵AD=ABAC=AF
∴△ADC≌△ABF（SAS）（6分）
∴∠AND=∠ABMDC=BF
又∵∠AND+∠DNA=90°
∴∠ABM+∠BNM=90°
∴∠NMB=90°
即DC⊥BF．（8分）
点评：本题考查了旋转的性质，解决此类问题的关键是正确的利用旋转不变量．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
26、如图，以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE，四边形ADFE是平行四边形．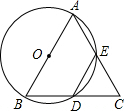
如图，以△ABC的边AB为直径作⊙O，交BC于D点，交AC于E点，BD=DE
（2011•峨眉山市二模）如图，以△ABC的边AB为直径作⊙O，BC与⊙O交于D，D是BC的中点，过D作DE⊥AC，交AC于点E．
（2010•黔东南州）如图，以△ABC的边BC为直径作⊙O分别交AB，AC于点F．点E，AD⊥BC于D，AD交于⊙O于M，交BE于H．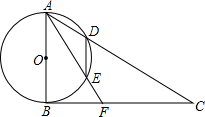
如图，以△ABC的边AB为直径的⊙O交AC于点D，弦DE∥AB，∠C=∠BAF