题目内容
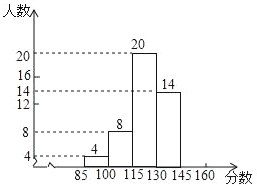
【题目】已知如图,在数轴上点A,B所对应的数是-4,4.
![]()
对于关于x的代数式N,我们规定:当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,代数式N取得所有值的最大值小于等于4,最小值大于等于-4,则称代数式N是线段AB的封闭代数式.
例如,对于关于x的代数式|x|,当x=±4时,代数式|x|取得最大值是4;当x=0时,代数式|x|取得最小值是0,所以代数式|x|是线段AB的封闭代数式.
问题:
(1)关于x代数式|x-1|,当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,取得的最大值和最小值分别是____ ______.
所以代数式|x-1|__________(填是或不是)线段AB的封闭代数式.
(2)以下关x的代数式:
①![]() ;②x2+1;③x2+|x|-8;④|x+2|-|x-1|-1.
;②x2+1;③x2+|x|-8;④|x+2|-|x-1|-1.
是线段AB的封闭代数式是__________,并证明(只需要证明是线段AB的封闭代数式的式子,不是的不需证明).
(![]() )关于x的代数式
)关于x的代数式![]() 是线段AB的封闭代数式,则有理数a的最大值是__________,最小值是__________.
是线段AB的封闭代数式,则有理数a的最大值是__________,最小值是__________.
【答案】(1)5,0,不是;(2)④,理由见解析;(3)a的最大值是2,a的最小值是-14
【解析】
(1)根据绝对值的性质可求最值,再根据封闭代数式的定义即可求解;
(2)根据封闭代数式的定义即可求解;
(3)分两种情况讨论:![]() +3≤4,
+3≤4,![]() +3≥-4,依此即可求解.
+3≥-4,依此即可求解.
(1)解:当x=-4时,|x-1|取得最大值为5,
当x=1时,|x-1|取得最小值为0,
∵|x-1|的最大值>4,
∴|x-1|不是线段AB的封闭代数式.
(2)证明:①∵-4≤x≤4,
∴2≤![]() x≤2,
x≤2,
∴![]() ≤
≤![]() x
x![]() ≤
≤![]() ,
,
∵![]() x
x![]() 的最小值为
的最小值为![]() ,不满足最小值大于等于-4,
,不满足最小值大于等于-4,
∴![]() x
x![]() 不是线段AB的封闭代数式.
不是线段AB的封闭代数式.
②当x=±4时,
代数式x2+1取得最大值17,不满足最大值小于等于4,
∴x2+1不是线段AB的封闭代数式.
③当x=±4时,
代数式x2+|x|-8取得最大值12,不满足最大值小于等于4,
∴x2+|x|-8不是线段AB的封闭代数式.
④当-4≤x<-2时,
原式=|x+2|-|x-1|-1=-(x+2)+(x-1)-1=-4,
当-2≤x≤1时,
原式=|x+2|-|x-1|-1=(x+2)+(x-1)-1=2x,
∴-4≤2x≤2,
当1≤x≤4时,
原式=|x+2|-|x-1|-1=(x+2)-(x-1)-1=2,
综上所述:-4≤|x+2|-|x-1|-1≤2满足最大值小于等于4,最小值大于等于-4,
∴|x+2|-|x-1|-1是线段AB的封闭代数式.
(3)![]() +3≤4,
+3≤4,
a≤|x+1|+2,
|x+1|+2在-4和4之间的最小值是2,a要不大于这个最小值才能使所有在-4和4之间的x都成立,
所以a的最大值是2,
![]() +3≥-4,
+3≥-4,
a≥-7(|x+1|+2),
-7(|x+1|+2)在-4和4之间的最大值是-14,a要不小于这个最大值才能使所有在-4和4之间的x都成立,
所以a的最小值是-14.

【题目】一张长方形桌子可坐6人,按下图方式讲桌子拼在一起.
 ………
………
① ② ③
(1)观察图形,填写下表:
图形(n) | ② | ③ | …… | n |
坐的人数(人) | …… |
(2)一家餐厅有40张这样的长方形桌子,按照上图的方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)在(2)中,若改为每8张桌子拼成1张大桌子,则共可坐多少人?
【题目】某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式 | 直接销售 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 100 | 250 | 450 |
现在该公司收购了140吨蔬菜,已知该公司每天能精加工蔬菜6吨和粗加工蔬菜16吨(两种加工不能同时进行)。
(1)如果要求在18天内全部销售这140吨蔬菜,请完成下列表格:
销售方式 | 全部直接销售 | 全部粗加工后销售 | 尽量精加工,剩余部分直接销售 |
获利(元) |
(2)如果先进行精加工,来不及精加工的进行粗加工,要求15天内刚好加工完这140吨蔬菜,则应如何分配加工时间?